Solving equations and inequalities

In this section we briefly review elementary methods used for solving equations and inequalities. We will focus on problems that can show up, the reader might be surprised to see how properties of functions come into play in this section. This section consists of parts Equations, Inequalities, Sign inequalities, Double inequalities, Splitting the real line, and (In)equalities with trig functions.

Consider an equation that features an unknown x. The usual way of solving equations is to isolate x on one side. In general we proceed by applying some operations to both sides of the equation, which works in many cases but sometimes we have to be careful, which is exactly the topic of this part. Everybody knows that we can add or subtract from both sides freely, but when dividing or multiplying an equation we have to be more careful, since this only works if we do not use zero for the dividing/multiplying.

What is not so widely understood is another trick that is often used. In many equations we have a function that we want to get rid of, for instance the equation ln(x) = 2 is of this type. The most efficient trick is to apply (to both sides) the inverse function to the one that we want to make disappear, the function and its inverse then cancel each other. The inverse function to logarithm is the exponential, so we do

e^ln(x) = e²,
x = e².

However, this is not always so easy. Consider the following two examples.

Example: Consider the equation arcsin(x) = π/2. We apply the inverse function.

sin[arcsin(x)] = sin[π/2],
x = 1.

Now consider this equation: sin(x) = 1. If we do the analogous procedure,

arcsin[sin(x)] = arcsin[1],
x = π/2,

we get a wrong answer. How is it possible? What is the right answer then?

The key to this trick is the notion of an inverse function. In the first example, the sine is the inverse function to arcsine on the interval [−1,1]. Is x really from this interval? In this case yes, since arcsin does not accept any other value, so the given equation itself already restricts x to the right region. We therefore deal with arcsin on the region where it is invertible and the formula works.

On the other hand, arcsin is not the inverse function to sine, but only to sine restricted to . Now there is no guarantee that the x in the equation is from that region, and for x from other regions we have different inverse functions. Finding the solution is therefore more complicated and in fact there are infinitely many correct solutions of the form π/2+2kπ, where k is any integer.

We have similar problem with roots. One way we get all solutions:

 = 3,
[]² = 3²,
x = 9.

It worked because the square is the inverse function to the square root on the interval [0,∞) and no other x are permitted in the given equation. The other way it does not work.

x² = 16,
[x²]^1/2 = 16^1/2,
x = 4.

Again, the problem is that to get inverse to square we need to restrict it to [0,∞), but now we have no guarantee that the x in the equation is from this region. The correct answer here is −4 and 4.

So far we had problems with missing solutions. It is also possible to get false solutions. In fact this is again related to the problem with inverses. We change an equation and find the solution of the new one, but how do we know that it is also a solution to the original equation? This is true if we can also go back, from the last form to the first (given) form of the equation. Therefore the operations that we do should also work in the opposite direction. In other words, if we have two functions that are mutual inverses only somewhere, then we have a trouble going one way and either it pops up on the way to the solution, or it may bite us going back. Look at this example.

(2-x²)^1/2 = x,
[(2-x²)^1/2]² = x²,
2-x² = x²,
2x² = 2,
x² = 1,
x = 1, −1.

It seems that we have two solutions, but only one works, namely x = 1. Note that no such problem appears when we work with logarithm and exponential, we would also be fine with cubic root and cubic power and any other pair of mutually inverse functions that do not require restriction. In other cases we have to be very careful, in particular it is crucial to always check that the solutions we obtained indeed satisfy the equation that we were given, in the original form.

There is no universal method for dealing with these problems. For popular functions we remember what is happening, for instance we should remember that the square root of x² is not x but |x|. Sometimes, if we have the existence of inverse functions only on parts of the real line, it helps to split the region where we solve to corresponding parts, see appropriate topic below.

With inequalities we can have all the troubles discussed above and some more. Again, we can add to/subtract from both sides of an inequality without trouble and we all know that when multiplying/dividing an inequality, we have to inquire about the sign of the number that we multiply/divide with. If this number is positive, then we keep the direction of the inequality, but if it is negative, we have to reverse it. If this term involves the unknown, then we do not really know the sign and we have to solve the inequality several times to cover all possible situations, see the part Splitting the real line.

When applying some function to inequality we have two troubles. One is about cancelling inverse functions, which causes similar problems as before. However, here we have to be careful already when applying a function to an inequality, because not every function can be applied to inequalities. The condition is simple. Only functions that are monotone can be applied; if the function we apply is increasing, we keep the inequality as it was; if the function we apply is decreasing, then we have to switch the direction of the inequality. And again, sometimes the function we apply is monotone only somewhere and things get even more interesting.

For instance, both logarithm and exponential are increasing functions everywhere. Thus we can solve the inequality e^x < 5 by applying logarithm to both sides without switching the direction, we get ln(e^x) < ln(5), that is, x < ln(5). On the other hand, x² is not monotone, so in general we cannot square both sides of an inequality, only under some special circumstances (for instance if we know somehow that both sides are positive, since on the positive half-axis the square is increasing).

For popular functions we have tricks for solving inequalities. If polynomials are involved, we can use approach via graphs or the trick described in the part Sign inequalities. Pictures help also when working with trigonometric functions, another approach is shown in the last part here.

By sign inequalities we mean inequalities where one side is 0, then the exact value of the expression on the other side is not importnant, only its sign. These inequalities can be solved quite easily if this other side can be expressed as a product and/or ratio of simple terms, because the sign of a product/ratio can be easily deduced from signs of its parts. Thus it is enough to investigate signs of individual factors and then put it somehow together.

With a bit of luck, every such simple expression is continuous and as a such it changes signs in a controlled way. Precisely, the real line splits into several regions on each of which this expression has just one sign, and the splitting points (where the signs change) are exactly the points where this expression is zero. Since in every given region the sign is the same everywhere, we learn it simply by picking some point from there and substituting it.

For instance, x² − 1 is zero at −1 and at 1, so the real line splits into regions (−∞,−1), (−1,1), and (1,∞). From the first we pick for instance x = −2, substitute and get 3 > 0, so x² − 1 is positive on the first region, similarly we learn that this expression is negative on the second region and positive on the last region.

From this we get the procedure for solving sign inequalities.

First we find zero points of all factors. Then we use them to split the real line into regions. For each region we find signs of every factor. This is done by picking some point from inside this region and substituting it into all factors. Then in every region we put together all signs of the factors using the sign algebra and obtain signs of the whole expression. In the last step we collect all regions where the sign satisfies the given inequality. If the inequality is sharp, we use open intervals. If it includes equality, then we include endpoints, but only if they do not cause trouble in the expression.

For linear factors it gets even easier, since linear factors change sign only once, at the point where they are zero, so for a particular linear factor we just mark the point where it is zero and then it is one sign everywhere to the right and the other to the left. To find which is which (whether the signs go − + or + −) we just substitute one point other than the zero point.

Sometimes we do not split the whole real line but just a part of it, this happens when some numbers are forbidden by the expressions in the inequality. This does not happen often (usually we just work with polynomials), but when it happens it is not really a problem, as you will see in the following example.

Example: Consider the inequality

We have one trouble here, logarithm only accepts positive numbers. The relevant inequality is x + 2 > 0, so right from the start we restrict our calculations to x > −2. Now we start the usual algorithm. First zero points. The equations 3 − x = 0, x + 5 = 0, x − 1 = 0, 2x − 1 = 0, ln(x + 2) = 0 have solutions x = 3, x = −5, x = 1, x = 1/2, and x + 2 = 1, that is, x = −1.

We order these points and then check how they split the region (−2,∞) where we are working; in particular we see that x = −5 does not fall there and thus it is irrelevant. We get regions (−2,−1), (−1,1/2), (1/2,1), (1,3), and (3,∞). To determine signs in these regions we use a table.

We want the expression to be positive, so the right regions are (−2,−1), (1/2,1), and (1,3). Since also zero is allowed by the inequality, we check which endpoints of these three intervals do not cause troubles. We see that −2 is out due to the logarithm, 1/2 and 1 make zero in the denominator, so the only point that works is 3. The answer is

(−2,−1) ∪ (1/2,1) ∪ (1,3].

Note that this inequality can be also solved by first getting rid of the fraction, which means that we would like to multiply both sides by the denominator. But for that we would have to investigate the possible signs of the denominator, consequently we would have to split the real line and solve several inequalitites (see the part Splitting the real line), most likely it would be much worse than this solution. Determining signs is usually the fastest way to go. Therefore we often transform also other inequalities into this type, for example like this.

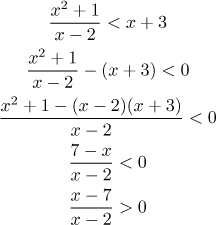
Splitting points are 2 and 7, we see that the solution is (−∞,2) ∪ (7,∞).

Double inequalities look like these two examples.

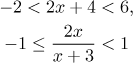
There are usually two possible ways to solve such double inequalities. One way is to solve them both simultaneously, by applying operations to all three sides. This is sometimes easy, for instance with the first example.

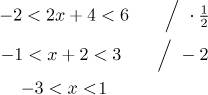
The solution is the interval (−3,1). However, the second example does not look so inviting. The first step would be to multiply all sides by the denominator x + 3, but since we do not know its sign, we would have to split the real line and solve the whole problem twice. We will show this procedure in the part below on Splitting the real line, you will see there that it is a bit longer.

The second possible way is to simply solve each inequality separately and then intersect the solutions (we want both inequalities to be true). This is often easier, especially if we can change the two inequalities into sign inequalities. That would be my preferred way for this second example. Recall that the "upside down-vee" sign denotes logical "and".

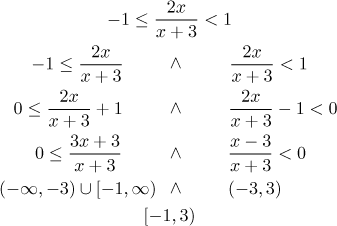
Often we are in a situation that we are solving an (in)equality but the step we are about to do requires a certain knowledge that we do not have, namely the sign of some expression. There are two most popular reasons for this, either we want to multiply/divide an inequality by some expression, or we want to get rid of an absolute value.

If this expression involves the unkown x, then we do not know its sign. Then we need to explore both possibilities for the sign, but each solution will work only on a part of the real line, the part where this expression has that particular sign. Thus we actually split the real line according to the sign we need and solve the problem in each part separately, at the end we take a union of the partial solutions. However, note that any result obtained while solving in one particular region is valid only within this region, that is, all parts outside of this region must be disregarded (in other words, any solution we get in a particular region must be intersected with this region before we use it further).

As an example we return to the second double inequality above. We would like to multiply the whole thing by x + 3, but for that we need to know the sign of it so that we know whether to switch the direction of the inequality. There are two possibilities and we need to explore both. We see that the expression is positive for x > −3 and negative for x < −3, which determines the regions into which we split the real line. Then we solve the problem in each region separately.

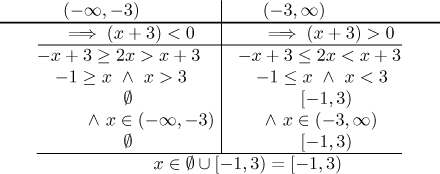
If we have more troublesome terms, we find dividing points for all of them and then make a universal splitting of the real line, so that on each region every troublesome term is already determined.

Example: Consider the double inequality

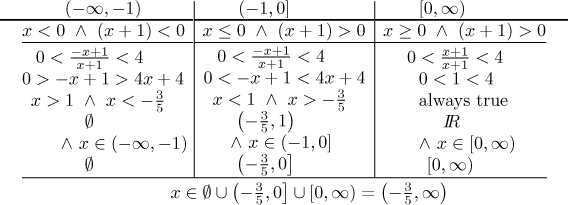
Again, note how in each region we intersected the solution we obtained there with that region, at the end we used union to connect all solutions.

Here we will just show one useful trick. The starting point here is simple (in)equalities like sin(x) = 1 or cos(x) < 1/2. The best way to solve such (in)equalities is to use the appropriate graph. Probably the easiest way is to first identify the solution within one period and then add periodicity to it.

For the first equality we would first conclude that on the first period of sine we have the solution x = π/2, then we add periodicity: x = π/2 + 2kπ.

The second example works similarly. From the picture we see that the solution is described by inequalitites π/3 < x < 4π/3, then we add periodicity:

π/3 + 2kπ < x < 4π/3 + 2kπ.

What do we do if the argument of the trig function is somehow transformed? Consider the inequality cos(2x + 1) < 1/2. How do we solve this? There are two popular methods.

One method is directly using a picture, but this time we need to draw the graph of cos(2x + 1). For an experienced student this should not be difficult to guess (see Transformations and graph guessing in Function - Methods Survey - Basic properties of real functions). However, it can be tricky, so some people (for instance me) prefer another way.

The second method uses the usual graph of the relevant trig function and first we pretend that there is just x in the argument. We find the solution just as we did before, but then instead of x we put the expression in the argument and solve for x. In our example it would go like this.

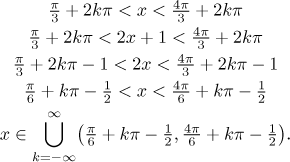
We expressed the answer using a set description, namely using an infinite union, but as you can see, once you have the solution described using inequalitites, it is easy to switch to intervals. The advantage of this method is that we can use it also for more general transformations that would be difficult to draw, for instance to solve inequalities like this: 0 ≤ tan(x²+1) < 1.