
Here we introduce mappings, look at their properties and introduce operations. At the end of this section we look at comparing sizes of sets.
Definition.
Consider sets A and B. By a transformation or a mapping from A to B we mean any subset T of the Cartesian productA×B that satisfies the following condition:For every a from A there is a unique b from B such that
(a,b)∈T. We write
T : A ↦ B.
Example: Consider sets
is a mapping from A to B.
We view such a mapping as a black box that sends elements from one set to another set, for instance the element a is sent to 1. The condition from the definition essentially means that one element from A cannot be sent to two (or more) different places in B. On the other hand, there is no problem in sending two elements to the same place, as you can see in the example. Note that it is not necessary to use up all elements from the target set B in the mapping.
This idea of sending is also reflected in a special notation we use for
mappings. Instead of saying that, say,
T : a ↦ T(a).
The starting set A is called the domain of T, denoted
Once we can send elements, we can also send sets. If D is a subset of A, the the image of D under T is the set
For instance,
Remark. Some authors also use the name function as an equivalent for a mapping. However, other authors reserve this name only for mappings that work with numbers, whereas the names mapping and transformation suggest a more general framework. This is the approach we adopt here, but since it is not a universally accepted convention, we will not make a big deal out of it.
There are two popular ways to draw mappings. One is the graph of
T, when we somehow mark which elements of the Cartesian product

In practice we usually do not bother drawing the unused elements of the product and use this picture instead.
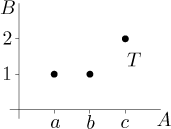
Drawing such a graph is probably the most popular visualization, but sometimes a different kind of a picture is more telling and therefore more useful.
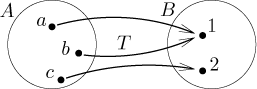
For ordered sets (especially sets of numbers) we often prefer this picture.
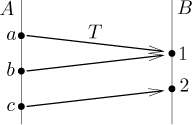
Before we move on we introduce one mapping that is always defined when we have a set.
Definition.
Consider a set A. We define the identity mapping on A, denotedIdA, as a mapping from A to A defined byIdA(a) = a for every a from A.
There are two important properties of mappings.
Definition.
Consider a mapping T from A to B.
We say that T is one-to-one (1-1), or injective, or that it is an injection, if for every two non-equal elements a1, a2 from A also their imagesT(a1), T(a2) are not equal.We say that T is onto, or surjective, or that it is an surjection, if
R(T ) = B. We say that T is a mapping "from A onto B".
The condition for injectivity says that two distinct elements cannot be sent to the same place. We have an advantage here that we do not pretend to be formally perfect, so we could say it this way. However, if we wanted to write it precisely and correctly using logical language, the definition would be more complicated than an alternative definition that goes like this. A mapping is 1-1 if the following condition is true: If two element are sent to the same place, then they must have been the same in the first place.
To a mathematician this statement is way neater, so it is used very often. It is also more convenient for practical work, since working with the relation "not equal" can get tricky, while we know how to deal with equalities.
Examples: In the following picture, the two examples of mappings in the first row are 1-1, while the three examples in the next two rows are not.

Now concerning surjectivity, the two examples of mappings in the first row are onto, while the three examples in the next two rows are not.
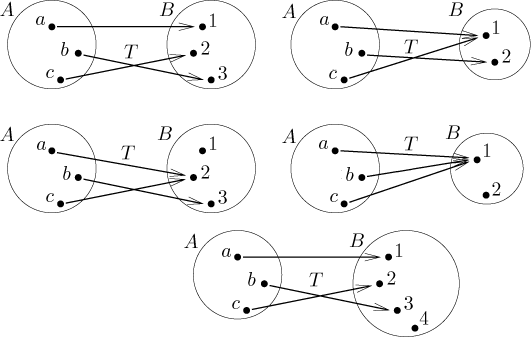
Note that sometimes these properties are determined by number of elements in the two sets. In the picture about injectivity, note that in the very last example we have no chance of creating a 1-1 mapping from A to B, simply because there are not enough elements in the target set. Similarly, in the picture about surjectivity, there is no way we can make a mapping onto B in the last example, since we cannot reach four elements with just three arrows. In general, if A and B are finite sets and the size of A is greater (sharply) then the size of B, then we cannot make a 1-1 mapping from A to B; on the other hand, there is no chance of surjectivity if the size of A is (sharply) smaller than that of B. We can also pass to counterpositives. If there exists a 1-1 mapping from A to B, then B must have at least as many elements as A. If there exists a mapping from A onto B, then A must have at least as many elements as B.
The above two properties combine into a very useful notion.
Definition.
Consider a mapping T from A to B.
We say that T is bijective, or that it is a bijection, if it is one-to-one and onto.
Among all the above examples there is just one bijection, namely the upper left example in the last (and second last) picture. Bijections are very useful, since they allow us to compare sets. For instance, from the above remark concerning sizes we should guess that for two finite sets, unless they have the same number of elements, they cannot be connected by a bijection; conversely, if there is some bijection, then the two sets must have the same number of elements. We look closer at this in the last part of this section.
Intuitively, if we have two sets and a bijection between them, then we have a pairing of elements of the two sets, and it seems that the direction of the arrows is no longer important. This is true, we will look at this in the next part.
We start with something very simple, it does not count as an operation, but it is something we can do to mappings.
Definition.
Consider a mapping T from A to B. Let D be a subset of A. We define the restriction of T to D as the mapping S from D to B defined byS(d) = T(d) for all d from D.
Intuitively, we simply pretend that T does not exist outside D
and we have the restriction. We denote it

Since the sets we work with here are general, there are no operations (like addition etc.) available. Thus the only thing we can try in general is to look at composition of mappings.
Definition.
Let T be a mapping from A to B and let S be a mapping from B to C. By the composition of these two mappings we mean the mappingS ○ T from A to C defined by
S ○ T : a ↦ S(T(a)) for a from A.
That is, we first find the image of a under T and then we substitute this image into S. The picture shows that it makes sense, since the images under T are exactly in the space where S works; precisely, the range of T is a subset of the domain of S.
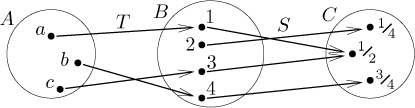
For instance,
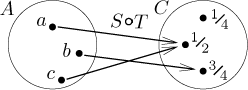
Note that the notation for composition is read "right to left", that
is, when substituting, we first use the function on the right and then the
one on the left. This may be unusual at first and beginners occasionally mix
it up, but it makes sense, since the order is the same as the alternative
notation
Note also that in such a composition the second mapping S only matters
at places where one can get to it using T; in other words, values of
S at elements of B that are not parts of
Fact.
Let T be a mapping from A to B and let S be a mapping from B to C.
If both T and S are1-1, thenS ○ T is also1-1.
If T is not1-1, thenS ○ T is also not1-1.
If both T and S are onto, thenS ○ T is also onto.
If S is not onto, thenS ○ T is also not onto.
If both T and S are bijections, thenS ○ T is also a bijection.
It might be interesting to think of some implications that suggest themselves
but are not listed above, obviously because they are not true. For instance,
the following picture shows that it can happen that S is not

On the other hand, in the previous picture S was not injective and nor
was the composition. This shows that if the injectivity fails for S,
then the injectivity of the composition
Once we have composition, we can pass to another important definition.
Definition.
Let T be a mapping from A to B. We say that a mapping S from B to A is the inverse mapping to T, denoted T −1, if
S(T(a)) = a for every a from A and
T(S(b)) = b for every b from B. If such an inverse mapping exists, then we say that T is invertible.
Intuitively, these two mappings cancel each other's effect. If T sends a someplace, then S sends it back where it came from, and vice versa.
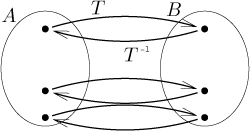
The symmetry in the above picture means that being inverse is in a sense a
symmetric notion, that is, also T is an inverse to
T −1, we can write it as follows:
Note that
Above we had lots of pictures with examples of mappings that were or where not 1-1/onto. If you think about them for a while, you should start having a feeling that it is not possible to "undo" action of a mapping if it is not one-to one or onto. In the first case two arrows go to the same place, so obviously it is not possible to create an arrow in the "opposite direction" for the inverse mapping and the first equality in the definition is not true. If T is not onto, then there is an element in B that is not a target for any arrow, thus making it impossible again to do an "opposite" arrow, this time the second condition in the definition fails.
Theorem.
Let T be a mapping from A to B. It is invertible if and only if it is a bijection.
Remark: If a mapping is a bijection, then it is invertible, by the above observation also its inverse is invertible and thus the inverse mapping is a bijection.
It is interesting to put the notion of inverse together with the composition. The condition in the definition of the inverse function can be rewritten as follows:
This suggests an interesting structure for the operation composition. If you are curious, look at this note.
Note that if a mapping from A to B is not onto, then there are some unused elements in B. In many situations we can disregard them, thus we get the following statement.
Theorem.
Let T be a mapping from A to B. If we consider it as a mapping from A toR(T ), then it is bijective (and therefore invertible) if and only if it is 1-1. Then it also has an inverse T −1 fromR(T ) to A.
If two sets are finite, we can compare their sizes by simply counting numbers of elements in each of them. As we saw above, we can also determine equality of their sizes by asking the following question: Does there exist a bijection from one set to another? This other way is used as a definition, since it works not only for finite sets, but also for infinite sets. Then we do not talk about sizes, but about cardinalities.
Definition.
Consider two sets A and B. We say that they have the same cardinality, denoted|A| = |B|, if there exists a bijection from A onto B.We say that the cardinality of A is less than or equal to the cardinality of B, denoted
|A| ≤ |B|, if there exists an injective mapping from A to B.
Equivalently,
This feeling that things work "normally" is further strengthened by
a statement called the Cantor-Bernstein theorem: If
We say that a set A is finite if either it is empty (then it
has cardinality 0) or there exists a positive integer n such that
A has the same cardinality as the set
As we observed above, for finite sets the notion of cardinality agrees with the intuitive notion of size. It gets more interesting when sets are infinite, since it turns out that there are many "sizes" of infinity. One of the most important "sizes" is the cardinality of the set of all natural numbers (see the next section).
Definition.
Consider a set A. We say that this set is countable if it has the same cardinality as the set ℕ of all natural numbers.
Countable sets are those sets whose elements can be "indexed" or
"enumerated". Indeed, consider a set A that is countable. By
definition, there must be some bijection T from A onto the set
ℕ. Now we can order
elements of A according to the number they are assigned via T.
First we take the element a such that
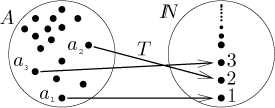
This property of being "indexable" is very useful, so countable sets are
very welcome, in particular such a set can be exhausted by induction.
By the way, countability is the smallest size of infinite sets. What
sets are countable? It turns out that quite a lot, since the "countable" size
of infinity can take quite a lot. We start with a simple observation that
adding one element to a countable set does not change its size. To prove
this, it is enough to show that the set of natural numbers has the same
cardinality as the set of natural numbers enriched by 0. The bijection we use
is
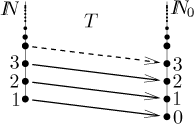
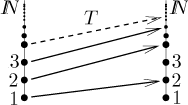
We see that adding one element to an infinite set does not change its size. We can do even better. If we enlarge a countable set by another set of the same size, it will still be countable. One way to see this is to prove that
integers form a countable set,
since we know that integers are formed by taking natural numbers and adding natural numbers with minus signs (cf. the next section). Intuitively we would say that there must be twice as many integers as there is naturals, but infinities are tricky.
First we need to make infinitely many holes in natural numbers to make room
for negative integers. Consider the mapping
This actually shows that the set of natural numbers has the same size as the set of even natural numbers, but for us the important thing is the holes on the right. There is obviously infinitely many of them, so they offer places where we can send negative numbers.

This particular T is defined as follows:
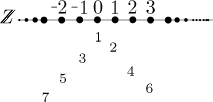
We index by keeping going left and right, obviously we will eventually index all integers in this way. By the way, this indexing exactly corresponds to the bijection above. We introduce this alternative reasoning here, because we will use it in proving the most outrageous claim so far: If we add infinitely many copies of natural numbers to this set, we again get a countable set. In other words, the Cartesian product of natural numbers with natural numbers has the same size as the original set. We will prove it by coming up with a way to enumerate all pairs. We will indicate the first few indexed pairs and then show the general pattern.
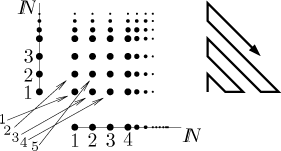
It seems clear that if we follow the pattern, we eventually index all the
pairs. We will now look at this result from two different points of view.
First, if we think of countable infinity as an abstract element, then the
first fact concerning countability shows that actually
We claim that
rational numbers form a countable set.
First, since rational numbers include natural numbers, it is clear that they are at least countable. Thus the more difficult part is in proving that they are also at most countable. Recall that we proved that the set of all pairs (a,b) of natural numbers is countable. Since we know that doubling does not change size of infinite sets, it follows that also the set
is countable. The mapping S defined by
Thus we see that all sets that we obtained by trying to fix some algebraic problems (cf. the next section) are countable. However, this is not true for real numbers.
Real numbers is not a countable set.
The classical proof of this fact shows that no matter how we try to enumerate real numbers, there will always be some left, and it is surprisingly simple, but still too long for this section; you have to take our word for it. Since connecting two countable sets yields a countable set and rationals are countable, it follows that there is uncountably many irrational numbers. In other words, when we look at a line in the plane, mark some point as origin and then mark all points whose distance from the origin is a rational number, then there will be substantially more holes than points on this line.
Cardinality of sets has been studied thoroughly for quite some time, there are sets that are even bigger than the set of real numbers and even bigger and so on (there is an infinite chain of infinite sizes), but one seemingly simple question remains open: Is the cardinality of real numbers the next after countability, or is there a set whose cardinality is strictly larger than countability but strictly smaller than cardinality of real numbers? Most mathematicians think that there is no intermediate size, which is called the Continuum Hypothesis, but nobody could prove it so far. If you happen to have an idea concerning this, you have a good chance to get some major math prize.