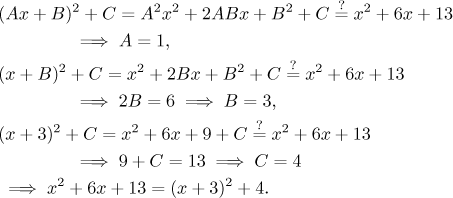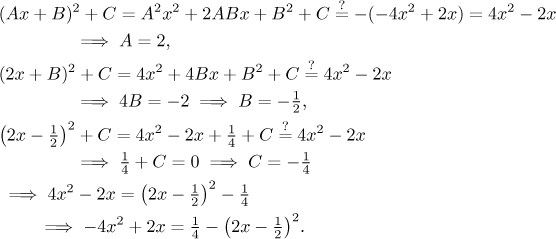Completing a square in a quadratic expression

The problem is simple: Given a quadratic expression ax² + bx + c, we want to rewrite it into the form (Ax + B)² + C. We use the knowledge of elementary algebra, namely we know that

(Ax + B)² = A²x² + 2Ax + B².

We will try to fit this to the given quadratic expression and it the only reasonable way is to start from the higest power.

If we want A²x² to be the same as ax², then there are two cases. If a is negative, then obviously this cannot be done and we leave it as a special case, see below. Otherwise we choose for A the square root of a. We get the following:

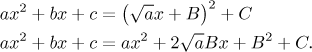
Now we need to make the linear factor fit, which gives us the equation

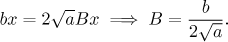
Now we have this:

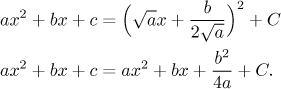
The powers of x all fit and it remains to choose C in such a way that also the constants are the same on the left and on the right, so

A simple example will explain it best. We will complete the square in x² + 6x + 13.

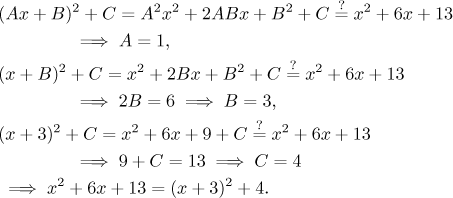
Case a < 0: Here we have to complete the square into the form C − (Ax + B)². We could derive a procedure for it, but it is much easier to simply complete square in minus the given expression according to the algorithm above, and then take the answer with minus.

As an example we will complete the square in −4x² + 2x.
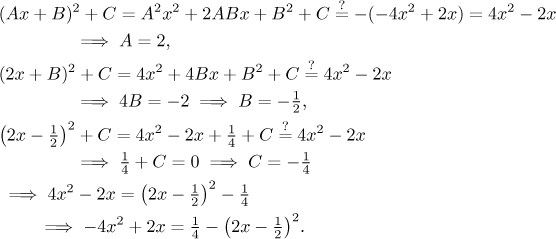
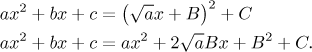
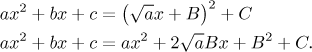
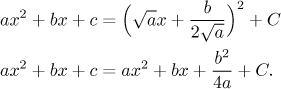