Functions of more variables: Derivative

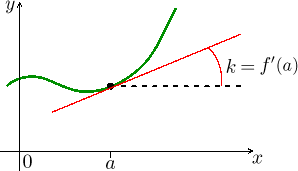
We start by recalling the major interpretations of derivative for a function of one variable. If we choose a certain value x = a for the variable, then the derivative f ′(a) gives the slope of the tangent line to the graph of f at the appropriate point. In applications we heavily use another interpretation, the value of f ′(a) tells us how fast the function f changes (rise or fall of the graph) when we pass through the point a (with unit velocity).

The third useful point of view tells us that using derivative we can approximate values of the function on some neighborhood of a using the tangent line, the formula is (two versions)

None of these interpretations works with functions of more variables. It is enough to look at a picture for the case of two variables: When we choose a point ∈D( f ) and stand at the corresponding point of the graph, it is not clear at all what a tangent line should be at that place. Also the answer to the question how fast the function grows or falls as we pass through is obvious: Depends which way we go, because unlike the case of one variable (left, right), here we have an amazing freedom of movement.

However, this observation brings us to one classical notion. If somebody does tell us in which direction to go from , then the question how fast the graph grows does make sense.

Example.
Consider the function f (x, y) = x² + y², we are at the point  = (1,2). What happens when we start off in the direction  = (h,k)?

We move on the line given by the parametric equation (x, y) = (1,2) + t(h,k), along the way we meet values

φ(t) = f (1 + th,2 + tk) = (1 + th)² + (2 + tk)² = (h² + k²)t² + (2h + 4k)t + 5.

This is just another example of slicing, as we saw it already in the first section. We cut the graph of f with a vertical plane above the line given by the formula t ↦  + t and expect to get a two-dimensional situation that we can handle.

Indeed, we have got a function φ of one variable that we can differentiate, the value of derivative at time t = 0 tells us how fast the value of the function changes while passing through the point .

Geometrically speaking, the graph of the function f was sliced by a vertical plane and this slice is now a one-dimensional situation where we easily determine the derivative.

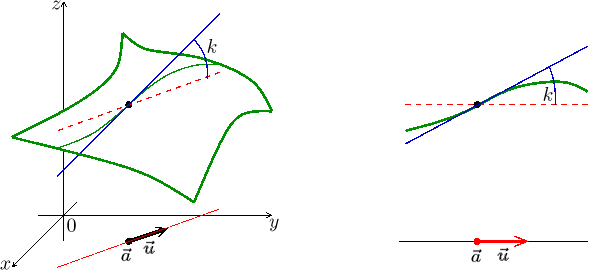
For instance, if we start off from the point in the direction  = (−1,1), then differentiating the corresponding function φ(t) = 2t² + 2t + 5 at time t = 0 we get number 2. What does it mean? It is the rate at which we see values of f changing while passing through the point . However, this is a relative quantity, depending on the speed at which we move. Since the directional vector is not of magnitude 1, our subjective slice does not coincide with the real slice through the graph; therefore also the result 2 has nothing to do with the change of the graph of f.

As we discussed, in order to get compatible results we have to use only directional vectors of size 1. In our case we would use the vector

Repeating the calculations above we find that in this direction, the graph of f is changing at the rate

This information now has a geometric meaning as well, for instance it gives the slope of a "directional tangent line", that is, the tangent line that we would construct using the real slice through the graph at .

Using the tangent line we are now able to approximate values of the function in the direction . For the function φ we have φ(t) ∼ φ(0) + φ′(0)t. If we use this with the normalized vector and pass back to f, we get the formula

Substition

leads to an equivalent but more pleasant formula

In fact, if we are interested in approximation that we need not normalize. The formula φ(t) ∼ φ(0) + φ′(0)t works for all (reasonable) functions φ, in particular we can apply it to φ corresponding to the original directional vector and we get the nicer form of approximation above right away.

In any case, the conclusion is that if we want to move from only in that particular direction, then we can approximate values of the function (for small s) using the formula

f (1 − s,2 + s) ∼ 5 + 2s.

Our thoughts lead to very useful ideas that deserve to be codified.

Definition.
Let f be a function defined on some neighborhood of a point ∈ℝⁿ. Let be a vector from ℝⁿ.

We say that the function f is differentiable at point in direction if the limit

converges.

Then we define the (directional) derivative of f at point in direction as

It is actually the derivative of the corresponding function φ,

which we can evaluate in the usual way. Even easier way will come soon.

Now we can express one of the results in the above example as D_(−1,1) f (1,2) = 2.

We did the definition for general directions , because in some applications (like physics) it makes sense, but here we will use only norm-one vectors.

In the first chapter we saw that cuts parallel with coordinate axes are more handy, because then we do not need to introduce a new parameter, we work with functions x ↦ (x, y₀,z₀,...), y ↦ (x₀, y,z₀,...) and so on, and directional vectors are of norm one so things are as good as they can get. These directional vectors are in fact the standard coordinate vectors ₁ = (1,0,...,0,0), ₂ = (0,1,...,0,0) through _n = (0,0,...,0,1), that is, the usual canonical basis of ℝⁿ.

So what do we get when we differentiate in the direction ₁, that is, along the x-axis? We work with the parametric formula x ↦ (x, y₀,z₀,...), obtaining the function φ(x) = f (x, y₀,z₀,...), that we want to differentiate with respect to x. We see that we do not really need any new function, it is enough to fix the other variables in f and differentiate by x in the usual way.

Example.
We return to the function f (x, y) = x² + y², we are interested in derivative in the y-direction at the point (1,2).

First we try it by definition. We move along the parametric line t ↦  (1,2) + t(0,1) with directional vector  = (0,1), giving rise to the function φ(t) = 1² + (2 + t)² = t² + 4t + 5. Then D f (1,2) = φ′(0) = 4.

Alternative approach: We take the function f (x, y), substitute 1 for x and differentiate the resulting formula f (1, y) = 1² + y² "with respect to y" in the usual way: [1 + y²]′ = 2y. Finally we substitute y = 2 and obtain the same result.

In such an easy way we can obtain derivative in arbitrary general point  = (x₀, y₀), for instance in the direction of the x-axis we find the derivative by differentiating the function x² + y₀², where y₀ is now some constant (unknown, but it is a fixed number). Since the derivative of the constant y₀² (although we do not know its value) is zero, we obtain 2x, therefore the derivative at (x₀, y₀) in the x-direction is 2x₀.

In real life calculations we do not write those subscript zeros, we simply say that the derivative of f (x, y) = x² + y² in the direction x is 2x and it is understood that this applies to arbitrary point (x, y). Similarly, derivative in the direction of the y-axis is 2y. And that's the whole secret.

Because these derivatives are so easy to derive and the axial directions are the most important, it is no surprise that this whole idea has a special name.

Definition.
Let f be a function defined on some neighborhood of a point ∈ℝⁿ. Consider unit vectors _i in axial directions, ₁ = (1,0,0,...,0), ₂ = (0,1,0,...,0), ..., _n = (0,0,0....,1).

For i = 1,...,n we define the partial derivative of f with respect to x_i as

if this exists.

In calculations we differentiate with respect to the given variable simply by imagining that the other variables (and expressions that they create) are constant and we differentiate by the given variable using the usual rules.

Example.
Consider the function f (x, y,z) = x²y + sin(y³ + 2z). We determine all partial derivatives.

We find the partial derivative with respect to x by imagining that y and z are some particular numbers. Since this is the first time, we actually show what happens when we really use some numbers for y and z, for instance 13 and π. Then sin(13³ + 2π) is also a number, that is, a constant. Differentiation thus yields

The same reasoning, but with "y" and "z" as constants, leads us to the result

Similarly, to get partial derivative with respect to y we imagine that instead of x and z there are constants, say 23 and π, and we run in our minds through the following calculation:

On paper we then write

Of course, an experienced derivator (as in "terminator") does not actually imagine numbers, he/she just learns to pretend that there are constants at the right places and analyzes the resulting expression. We still owe you the derivative by z, for that we take x and y to be constants, then also the whole term x²y is constant. Therefore

By the way, the curved sign ∂ that surprisingly does not have a short name (well, you can call it "partial derivative mark") can be used just like the usual derivative mark to indicate derivative of a particular expression, but here we write it from the left. For instance, in the last calculation above we can indicate aplication of the chain rule as follows:

The meaning of partial derivatives

We already know that partial derivatives tell us how the function changes (grows, falls) in key directions.

In this picture, both partial derivatives are negative, so the graph of this function goes down as we move from in directions of coordinate axes. It might seem that in other directions, a function is free to do whatever it wants, and that is true in general. However, if we demand that the graph of the function does not "break sharply", then it looses this freedom. It may surprise that relatively mild assumptions on the function already guarantee that its growth and fall in other directions is completely determined by its behaviour in axial directions.

Theorem.
Let f be a function defined on some neighborhood of a point ∈ℝⁿ. If there exists some neighborhood of on which partial derivatives exist for all i = 1,...,n and they are continuous at , then f has directional derivatives at in all directions and for every the following is true:

The requirement on continuity of derivatives is often satisfied, essentially every function given by an algebraic formula with elementary functions (apart from absolute value) fits in, and for such functions we can deduce derivative in arbitrary direction purely from knowing partial derivatives. This means that the condition of continuous derivatives has a rather large impact.

For convenient manipulation we usually gather all partial derivatives into one packet.

Definition.
Let f be function defined on some neighborhood of a point ∈ℝⁿ. If all partial derivatives () for i = 1,...,n exist, then we define the gradient of f at as the vector

It is worth noting that gradient is a vector from ℝⁿ, that is, we see it as an object from the function's domain; on a symbolic graph we see it within the horizontal representation of D( f ).

For a function with continuous derivatives (in other words, for most functions we normally meet) we can now express the conclusion of the above theorem in an elegant way using dot product,

D f () = ∇ f ()•.

Example.
Consider f (x, y) = x² + y². again. We already found its partial derivatives, so we readily write the gradient ∇ f (x, y) = (2x,2y).

At the point  = (1,2) then ∇ f (1,2) = (2,4) and formula gives D f (1,2) = ∇ f (1,2)•(h,k)=2h + 4k, exactly as we obtained it before using direct calculations.

Gradient carries lots of interesting information, it is one of key notions.

Gradient and slope.

Imagine that we are at a point , sitting on the graph and looking around. Depending on which direction we look at, the graph rises or falls. The rate at which it changes is given by the directional derivative. In other words, it is given by the expression ∇ f ()•, where are unit vectors. According to a well-known formula,

∇ f ()• = ||∇ f ()||⋅||||cos(α) = ||∇ f ()||cos(α),

here α is the angle between the vectors ∇ f () and .

We see that we will climb fastest if we start off so that cos(α) = 1, which happens for α = 0, that is, in the direction of the gradient. Conversely, the steepest fall happens when cos(α) = −1, in exactly the opposite direction.

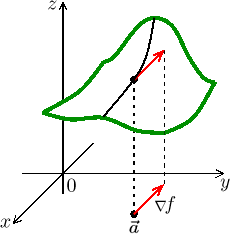
Fact.
Let f be a function that has continuous first partial derivatives on some neighborhood of a point . Then the gradient ∇ f () is the direction of the steepest growth of the function f at , the function increases at the rate ||∇ f ()|| there.

The vector -∇ f () is the direction of the steepest descent at .

Gradient and level sets.

We are still at a point and sitting on the graph. A certain level surely passes through this point of the graph, namely the level c =  f (), so the point lies on the corresponding level set (which is situated in the domain). If we start off from the point in exactly the same direction that the level set goes, denote it , then we surely expect that for at least a little while the value of f does not change (an infinitely small little while if you like differentials). This means that D f () = 0, that is, ||∇ f ()||cos(α) = 0, meaning that α = .

In other words, the direction at which the appropriate level set starts off from the point is perpendicular to the direction of fastest ascent given by the gradient. Try to imagine this practically. We are standing on a mountain side, thinking which way to go. Is it really necessarily true that the direction of sharpest climb is perpendicular to the direction of level walk? I can easily imagine mountains shaped in such a way that this would not be true. However, the trick here is that such mountains, considered as graphs of functions of two variables, would not have continuous derivatives there.

Fact.
If a function f has continuous first partial derivatives on some neighborhood of a point , then the gradient ∇ f () is perpendicular to the level set passing through .

This is very useful. Many objects can be represented as level sets for suitable functions, then the gradient allows one to easily obtain normal vectors to such an object.

Example.
Consider the ellipse given by the equation

we want to find its tangent line at the point (2,1).

One possible approach is through graphs. The given point lies on the upper half of the ellipse, where it can be viewed (after solving the formula for y) as the graph of the function

To find the tangent line at x = 2 we need the derivative

slope of the tangent line is therefore k = f ′(2) = −1. We obtain the line y − 1 = −(x − 2), that is, x + y = 3.

Alternative approach: We rewrite the given equation into a more pleasant form x² + 2y² = 6 and decide to see it as the level curve of the function F(x, y) = x² + 2y² corresponding to c = 6. We find the gradient at (2,1): ∇ F = (2x,4y), therefore ∇ F(2,1) = (4,4).

This vector is perpendicular to level sets, therefore also to the ellipse, therefore also to its tangent line. The equation of the line perpendicular to (4,4) is 4x + 4y = d, using the point (2,1) we easily find d = 12. We obtain the equation 4x + 4y = 12, that is, x + y = 3.

Gradient and tangents, approximation.

We already mentioned that with functions of more variables it makes no sense talking about tangent lines. However, when we imagine the graph of some function of two variables, it seems that there could be tangent planes. For functions of three variables there should be tangent three-dimensional spaces (they look "flat" when placed in the four-dimensional space where the graph lives) and so on. In general, a flat n-dimensional object in ℝⁿ⁺¹ is called an (affine) hyperplane (formally we mean translations of n-dimensional subspaces) and we are looking for special ones.

How do we find them? By leaving the world of geometry for the moment and turning to analytical approach. We know that with functions of one variable, the tangent line at a is the line that better than any other line approximates behaviour of f around a,

f (a + h) ∼  f (a) + f ′ (a)h.

How could we best approximate values of a function f (x, y) around a point  = (a₁,a₂)? Assume that we move a tiny bit away from this point, namely by a vector  = (h,k). How much does function change?

Instead of one "diagonal" movement we can arrive at the place (a₁ + h,a₂ + k) by first moving by h along the x-axis and then by k in the direction of the y-axis. But now the first movement is a one-dimensional affair, we change only one variable, and we know how to estimate the corresponding change in a function, we use differentiation in the appropriate direction:

From the point (a₁ + h,a₂) we now move in the direction of y-axis by k and similarly estimate

We put it together:

In the picture (we see the graph from below) we marked values used in approximation using filled circles, whereas correct values are marked with empty circles. We have also shown the tangent lines that we used.

If the function f is sufficiently nice, then the derivative does not change much when we move by a really tiny bit, so we can ignore the shift by h in the argument and write

In other words,

The expression on the right defines a plane and it is exactly the one we were looking for. Its equation is

or

It is a plane determined by the normal vector

Similar reasoning works in more dimensions, we have the estimate

and tangent hyperplane

Also here we get the standard form of equation by multiplying out.

Fact.
Let a function f have continuous first derivatives on some neighborhood of a point . If we extend the vector ∇ f () by one coordinate, namely we add −1 as the (n + 1)th coordinate, we obtain a vector from ℝ^n + 1 that is perpendicular to the tangent hyperplane to the graph of f at the point .

Example.
Consider f (x, y) = x² + y² and the point (1,2). We find the tangent plane to the graph of f at the corresponding point.

We have already found ∇ f (1,2) = (2,4). As a normal vector to the graph we can therefore take  = (2,4,−1).

Through which point should the plane go? Since f (1,2) = 5, the point is (1,2,5). We have a point and normal vector, the equation of the plane follows easily:

0 = •((x, y,z) − (1,2,5)) = 2(x − 1) + 4(y − 2) − (z − 5)   =>  2x + 4y − z = 5.

Alternative: Plane perpendicular to the vector (2,4,−1) has equation 2x + 4y − z + d = 0. Substituting in the point (1,2,5) we get d = −5, hence 2x + 4y − z − 5 = 0 is the equation.

Another alternative: The graph is given by the equation z = x² + y². Rewriting it as x² + y² − z = 0 we can treat it as the level surface of the function F(x, y,z) = x² + y² − z corresponding to the value c = 0. We easily find ∇ F = (2x,2y,−1) and we know that the vector ∇ F(1,2,5) = (2,4,−1) is perpendicular to this level surface, therefore also perpendicular to the graph and in particular to the desired tangent plane. Its equation is therefore

2(x − 1) + 4(y − 2) + (−1)(z − 5) = 0

and we are done.

Conclusion: The tangent plane to the graph of f at the point given by  = (1,2) has the equation 2x + 4y − z = 5.

We use this example to review other uses of gradient.

The function f grows fastest when we leave the point (1,2) in the direction (2,4), that is, in the direction (1,2) (every positive multiple of a vector has the same direction), the rate of growth then will be

The point (1,2)∈ D( f ) lies on the level curve f (1,2) = 5, that is, on the circle given by the equation y² + x² = 5. At the point (1,2) the vector ∇ f (1,2) = (2,4) is perpendicular to this curve, which allows us to easily write the equation of the tangent line to this circle:

0 = ∇ f (1,2)•((x, y) − (1,2)) = 2(x − 1) + 4(y − 2)   =>  2x + 4y = 10.

Using the normal direction (1,2) and the popular trick we can obtain a vector from ℝ² tangent to the circle, for instance (2,−1).

Partial derivatives of higher order

Just like with functions of one variable, also functions of more variables can be differentiated more times (if they allow us). For instance, with the function f (x, y) = |x + y| already the first partial derivatives fail at the point (0,0), on the other hand on every reasonably small neighborhood of the point (3,2) we can differentiate it as many times as we want, since in places where x + y > 0 we have f (x, y) = x + y.

However, unlike the case of one variable, here we have a choice regarding what to differentiate and with respect to which variable. A function of two variables has first order derivatives and and they both can be in turn differentiated by x or by y, obtaing four distinct partial derivatives of order two, for instance the following two. We will show first a detailed record of the procedure and then the standard condensed notation:

Note the order of differentiation: The symbols in the denominator are read from right to left, so we start with derivative by the variable most to the right. For instance, in the partial derivative of third order 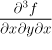we would first differentiate f with respect to x, then the result is differentiated by y and this by x again, whereas to obtain we would first differentiate with respect to y and then twice by x.

Definition.
Consider a function f defined on some neighborhood of a point ∈ℝⁿ. Let i₁,i₂,...,i_m∈{1,2...,n} be some indices of variables. We define the corresponding partial derivative of order m of the function f by induction as follows:

assuming that all derivatives that are needed exist.

If all the coordinate indices i_k are not the same, then we call this derivative a mixed derivative.

Just like derivatives of order one, the higher ones can also be collected into packets.

Definition.
Assume that a function f has all derivatives of order two at a point . Then we define its Hess matrix at as

Practically speaking, we differentiate the function f by its first variable, this derivative is then repeatedly differentiated once more, by all available variables, and the results create the first row of the matrix, similarly we create the other rows. Note that on the diagonal we have derivatives of the type , away from the diagonal there are the mixed derivatives.

To collect derivatives of the third order we would need a three-dimensional matrix, which brings us to tensors, a topic that we definitely do not want to explore here. In many (most?) applications we can do with the first two derivatives, we settle for them here as well.

There are actually quite a few partial derivatives, for instance, if we work with a function of three variables, then we are looking at 3⁴ = 81 partial derivatives of the fourth order. This sounds like a lot of work. Fortunately there is an interesting statement that makes our life easier.

Theorem.
If a function f has all partial derivatives of order m on some neighborhood of a point and they are all continuous at , then the order of differentiation makes no difference when calculating derivatives up to the order m.

This for instance means that if the function f is at least a bit reasonable (for instance given by a formula put together from elementary functions), then the Hess matrix is symmetric. This allows for some saving on work. When finding second order derivatives of a function of two variables, it is enough to find three instead of four, this is actually not so great and we often calculate all four anyway, since the match of the two mixed derivatives serves as a validity check.

We get better savings when it comes to derivatives of higher order. For a function of two variables it suffices to find four third-order derivatives instead of eight, for a function of three variables it means 10 derivatives of third order instead of 27 and 15 instead of 81 for order four. Actually, this is more of a theoretical saving, since we rarely go higher than second order in applications, but it is a nice thing to have anyway.

The meaning of higher order derivatives

We know that for a function of one variable, the second derivative determines its concavity: The sign indicates concavity up or down, the magnitude of the derivative tells us how sharp the bend is. This is where most courses stop. Just to satisfy our curiousity we mention that the third derivative determines the development of concavity as we scan the graph from the left to the right. Positive third derivative means that looking from left to right we see the curve's bend "tightening up", as if we were approaching the centre of a snail's spiral, whereas a negative third derivative signifies relaxation of the bend. We will not even attempt to give geometric interpretation of higher orders.

As usual, things get more complicated once we pass to more variables, so we just look at derivatives of the second order. This is already a bonus as this topic is traditionally ignored in common calculus courses.

The derivatives that are not mixed are the easy part. If we slice a function's graph in the direction of the x-axis, then determines concavity of the cut, just like we are used to, similar information comes from , , etc.

On the picture we see an interesting situation, in one direction the function is concave up and in the other it is concave down. This sends mixed signals about behaviour of the function there and brings us to the question: Is it true that just like with growth, the curving of the graph in other directions is already determined by its concavity in axial directions? Is it for instance true that if we investigate some function f (x, y) at a point and obtain positive and , then the graph should already be "concave up in all direction", that is, we expect a dimple at that place?

Surprisingly, the answer is negative, there can be many things going on, even in cases when the function has continuous derivatives of all orders. This shows that it is not a question of quality of the function, but rather a consequence of the fact that the non-mixed second order partial derivatives do not carry enough information. In other words, once we start investigating the curving of the graph, it is not enough to just look at what happens along the axes. We need extra information, and this is when the mixed derivatives come into play.

We first look at the derivative

and assume that it is positive. The second derivative we apply is by y, that is, we move in the direction of the y-axis. While moving this way, we have

which means that the function grows, that is, the slopes of tangent lines in direction x are increasing, meaning that these tangent lines are getting steeper.

Can you imagine a situation when you move in the y-direction and tangent lines taken in direction x are turning towards faster growth? Such a graph must be twisted, and that is the meaning of the second mixed derivative, it is the direction and measure of the graph's twist. We will show it on a picture where we look at behaviour at the origin.

To simplify the situation we chose a function that is constant along the axes, which (among other things) means that

We therefore see directly the influence of the mixed second derivative. To see the shape best, we turned the graph so that the x-axis goes to the right, as we are used to when drawing tangent lines. But then the y-axis must necessarily go away from us.

If the function is sufficiently smooth, then we should have

so we should get the same picture also when interpreting the expression

When we move in the x-direction, the slopes of tangents taken in the y-direction are increasing, lines are twisting up. The picture fits well, larger slopes of "y-tangents" means steeper growth in the direction of the y-axis, that is, away from us.

Deformation of a graph of this sort is the reason why concavity information in axial directions does not determine the whole shape. When investigating a graph, we have to compare (in a mathematical way) the convexity influence of non-mixed derivatives and the twisting action as indicated by the mixed derivative. Thus all the information in the Hess matrix comes into play, all entries (all derivatives of the second order) play a role of equal importance. Obviously, this topic shows up in the section on local extrema.

Functions of more variables: Local extrema
Back to Extra - Functions of more variables