NumericalMethods[IntNumeric] - approximates the value of a definite integral
Calling Sequence
IntNumeric(f, x=a..b, method=m, options)
Parameters
f - algebraic; expression with variable x, function to be integrated
a..b - range(numeric); the integrating range
m - name; method to be used
options - (optional) parameters of the form keyword = value, where keyword is one of stepsize, numsteps, output, romberg, panels, points, silent, plotops. One of the options stepsize, numsteps must be used.
Description
The IntNumeric command approximates the value of the definite integral of f(x) over the interval [a,b] using basic methods (rectangles, trapezoids, Simpson formula) and the Romberg integration. Its main purpose is to exhibit behaviour of basic methods and be accessible to students not versed in Maple. Acordingly, the main focus is on ease of use and informative output, not performace. Controls are similar to other procedures in the package.
The user must specify the step of the chosen method either directly or by specifying the number of intervals in a partition.
This command is part of the NumericalMethods package, so it can be used in the form IntNumeric(..) only after executing the command with(NumericalMethods). However, it can always be accessed through the long form of the command by using NumericalMethods[IntNumeric](..).
Options
method = left, right, midpoint, trapezoid, simpson, or simpson38
- left: the method of left rectangles (left rectangle composite formula).
- right: the method of right rectangles (right rectangle composite formula).
- midpoint: the method of midpoint rectangles (height of each rectangle is determined by the value of f in the middle of the relevant strip, so unlike the other methods it does not use partition points).
- trapezoid: the trapezoid method (trapezoid composite formula).
- simpson: the Simpson method (Simpson composite formula). The number of partitions must be even.
- simpson38: the Simpson 3/8 method (Simpson 3/8 composite formula). The number of partitions must be divisible by 3.
The options argument can be one or more of the following equations.
stepsize = positive
Determines the step size for the iteration. If necessary, the given value is corrected to the nearest step size that can be obtained using
numsteps = posint
Determines the number of steps (number of intervals in partition) used for the iteration; the step size is then set accordingly and reported by the procedure when output = information. If numsteps is not specified, the option stepsize must be used.
output = value, information, totalerror, or graph
Specifies what information is given by the procedure.
- value returns the approximation of the integral by the chosen method.
- information returns the approximation of the integral by the chosen method. Before that it prints additional information. If the stepize was determined by the procedure, its actual value is reported. The error of the integral approximation is shown. If Romberg integration was chosen, both integral approximations by the chosen method are shown and the Romberg error estimate.
- totalerror returns the error of the integral approximation (of the chosen method or the Romberg integration if specified).
- graph returns the plot of the given function (always in black) and the approximating panels with evaluated function points (red by default).
The default value is output = value.
romberg = posint
If romberg = k is specified, Romberg integration is used. The chosen method is used to approximate the integral with steps n and k*n. These two approximations are combined using Romberg integration to produce the returned final approximation. When output = information is specified, the two approximations by method are shown and the Romberg error estimate for the latter as well.
panels = on or off
Determines whether the vertical lines separating approximating panels should be shown when output = graph.
The default value is panels = on.
points = on or off
Determines whether the function values used in determining panels should be shown when output = graph.
The default value is points = on.
silent = on or off
Controls whether the procedure should report the value of stepsize if it has been set based on numsteps or redefined to fit the range.
- on: such instances are not reported.
- off: such instances are reported.
The default value is silent = off. The stepsize is always reported when output = information.
plotops = list
These options are passed to plotting commands if output is set to graph. Some options are overridden by the procedure: the legend is supplied automatically and the function is shown in black.
Examples
Default behaviour:
> IntNumeric(sin(x), x=0..Pi, method=left, numsteps=40);
Using step size 0.078540.
1.998971811
When we use a "nice" step for integrating range of irrational length, it will be surely adjusted and reported by default. We use output = information to see more information.
> IntNumeric(sin(x), x=0..Pi, method=midpoint, stepsize=0.1, output=information);
Using step size 0.101342.
The error of this approximation is 0.000856102.
2.000856102
If we want to work with the error further, we may ask to get it as return. For instance, we may use it to guess the order of the method. Now we do not want to se reporting on step size and supress it.
> IntNumeric(sin(x), x=0..Pi, method=trapezoid, numsteps=40, silent=on, output=totalerror);
IntNumeric(sin(x), x=0..Pi, method=trapezoid, numsteps=3*40, silent=on, output=totalerror);
q:=log[3](%%/%);
0.001028189
0.000114233
2.000081450
This worked quite well. Now we will try the two basic methods of order 4. We have to make the partition number divisible by both two and three.
> IntNumeric(sin(x), x=0..Pi, method=simpson, numsteps=42, silent=on);
IntNumeric(sin(x), x=0..Pi, method=simpson38, numsteps=42, silent=on);
2.000000348
2.000000783
We know that the Simpson method can be thought of as the outcome of Romberg integration applied to the trapezoid method. Let's see.
> IntNumeric(sin(x), x=0..Pi, method=trapezoid, romberg=2, numsteps=21, output=information);
Using step size 0.149600.
Approximation of the integral by the chosen method with n=21 is 1.996268599.
Approximation of the integral by the chosen method with n=2*21 is 1.999067410.
The Romberg error estimate of the latter integral approximation is 0.000933.
2.000000347
Close enough. The Romberg estimate for the error of T(42) is also very good.
Now we show the default graphical output and then modify it using plotting options. We provide step size that fits, so it will not be redefined and its value will not be reported.
>
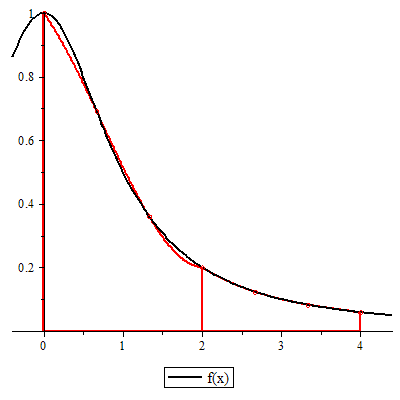
IntNumeric(1/(x^2+1), x=0..4, method=simpson38, stepsize=2/3, output=graph);

> IntNumeric(1/(x^2+1), x=0..4, method=simpson, stepsize=2/3, output=graph, plotops=[color=blue,symbol=box,symbolsize=13]);
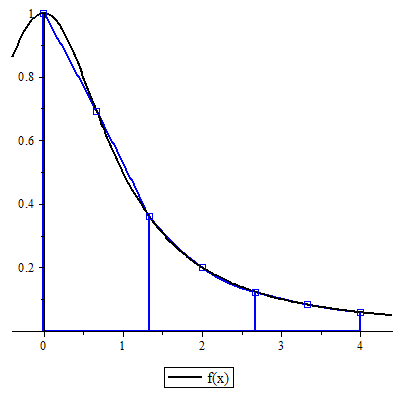
> IntNumeric(1/(x^2+1), x=0..4, method=midpoint, stepsize=2/3, output=graph, panels=off, points=off, plotops=[thickness=1,color=gold]);