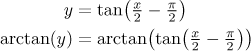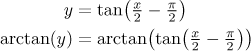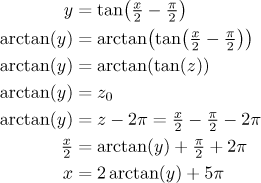17: Solving for x you should get
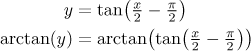
The problem now is that for a general z the expression
arctan(tan(z)) does not give z but some z0
from the basic interval of invertibility of tangent. If there is some
integer k such that
z − kπ
is from this basic interval, then
z0 = z − kπ,
the picture should explain it best.
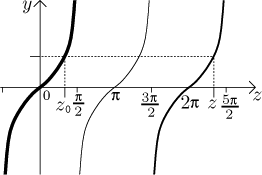
In our case we have to first observe that
z = x/2 − π/2
is from the interval
(3π/2,5π/2).
Thus
z − 2π
works, so
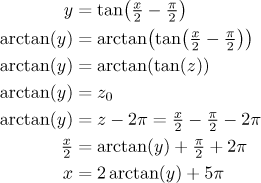
Answer