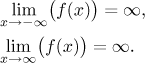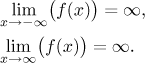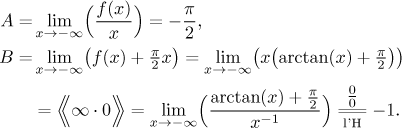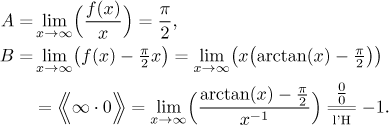35: D( f ) = ℝ; f is continuous there.
y-intercept: f (0) not possible; x-intercepts: f = 0 not possible.
f (−x) = f (x), hence f is even.
Limits at endpoints:

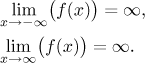
Interpretation as asymptotes:
No horizontal asymptote at −∞, but a chance for oblique.

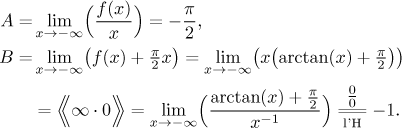
Asymptote y = −(π/2)x − 1 there.
No horizontal asymptote at ∞, but a chance for oblique.

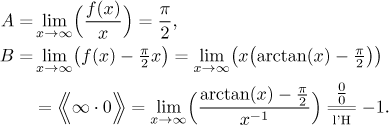
Asymptote y = (π/2)x − 1 there.

Now determine monotonicity using f ′.

Next hint
Answer