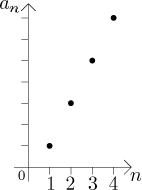
Grafy posloupností, které používáme, jsou inspirovány formální definicí: že posloupnosti jsou jakýsi druh funkcí. Proto začínáme s dvěma osami. Naše intuice o posloupnostech je ale odlišná: Představujeme si je jako hromadu čísel jdoucích jedno po druhém. Jako takové bychom je měli být schopni zakreslit jen pomocí reálné osy.

Jako příklad se znovu podíváme na {2n − 1}_n=1,2,3,.... Měli jsme tento graf:

Když teď ale vidíme posloupnost jako hromadu čísel {1, 3, 5, 7,...}, můžeme ji zkusit nakreslit jinak. Stačí jen jedna osa, reálná osa, naní členy posloupnosti vyznačíme a poznamenáme jejich pořadí:

Podobně lze příklad {3, π, 2, 2, −1, 0, −1, 0, 2.5,...}, n = 0,1,2,... nakreslit takto:

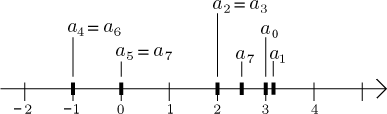
Tento způsob kreslení je často výhodnější, zvlášť když dojde na míchání posloupoností s funkcemi. Má nicméně jednu něvýhodu. Pokud jsou členy posloupnosti velmi blízké, obrázek bude příliš natlačený na to, aby ukázal něco užitečného.

Trocha přemýšlení by vás měla přesvědčit, že z tohoto druhu obrázku se dají hravě poznat základní vlastnosti. Omezené posloupnosti musí zůstat mezi dvěma mezemi:

Neomezené posloupnosti utečou, například tato není omezená zdola (což teď vypadá jako "zleva", ze záporného směru):

Rostoucí psloupnosti musí jít zleva doprava, klesající posloupnosti musí jít zprava doleva. Oscilující posloupnosti poskakují doleva a doprava.

Jak je tomu s limitou? Jestliže a_n konverguje k L, pak se přirozeně značky jednotlivých členů musí přibližovat značce pro L.

Definici a hru lze také dobře reprezentovat. Tolerance ε je prostě zaznačena okolo L a abychom vyhráli, musí se najít index (bod odříznutí) N tak, aby a_N a všechny následující členy zústaly v mezích dané tolernce.

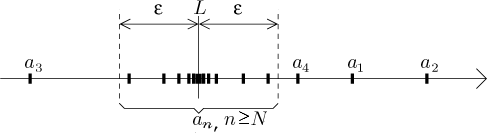
Tento obrázek vlastně naznačuje alternativní způsob, jak vyjádřit epsilonovou definici, kterou jsme dříve zavedli:

Definice
Uvažujme posloupnost {a_n}. Řekneme, že reálné číslo L je limita této posloupnosti pro n jdoucí do nekonečna, jestliže pro každé ε > 0, pouze konečný počet členů a_n zůstane mimo oblast (L + ε,L − ε).