Box "comparison and oscillation"

There are several ways to use comparison to find limits. There are two one-sided comparisons possible:

1. Consider two sequences {a_n} and {b_n}. If a_n ≤ b_n for all n and a_n→∞, then also b_n→∞.

2. Consider two sequences {a_n} and {b_n}. If 0 ≤ a_n ≤ b_n for all n and b_n→0, then also a_n→0.

To obtain non-zero limits by comparison, one needs two bounds:

The Squeeze theorem:
Consider three sequences {a_n}, {b_n}, and {c_n}, such that

a_n ≤ b_n ≤ c_n

for all n. If {a_n} converges to some L and {c_n} converges to the same L, then necessarily also {b_n} converges to this L.

The Squeeze Theorem - absolute value version:
Consider two sequences {a_n} and {b_n} such that

|b_n| ≤ a_n

for all n. If a_n→0, then also b_n→0.

We used here the most popular versions, for details see Theory - Limits - Limit and comparison.

Before giving a general overview of the comparison method we will show some examples. The above statements about comparison are used most often for one of the following three reasons:

Reason 1. The sequence we are investigating features an expression that does not have a limit but is bounded - that is, an expression that oscillates. The most typical examples are

The boundedness suggests the squeeze: an upper and lower bound for the given sequence.

Example: We will show that

We see that the expression in the numerator has an oscillating part, but we have a bound for it. We use this bound to deduce an upper and lower bound for the whole sequence:

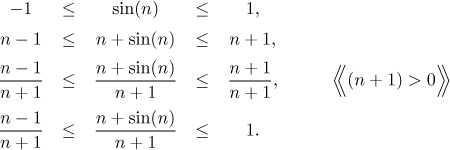
We made a note about n + 1 being positive, since this means that the direction of the inequalities does not change when dividing by this number.

The sequence on the left converges to 1. This can be easily seen by cancelling n; after all, this problem is a textbook example of a ratio of polynomials, see the box polynomials and ratios with powers.

The sequence on the right also tends to 1 (that is trivial). By the Squeeze theorem, the given sequence also converges to 1.

Reason 2. Most limit problems are solved by passing to functions, very often we use l'Hospital's rule. However, this sometimes fails already from the start, when we cannot pass to function. Typical example is powers with negative bases like (−2)ⁿ, also the factorial n!, where we do not really know how to change it into a function (although this can be done, see the Gamma function) and how to take a derivative. Thus one has to try an alternative approach, comparison often helps.

Example: We will prove that

Since the ratio is positive and we are trying to show that it tends to zero, we will use one-sided comparison for it and try to find some suitable upper estimate. Note that we are looking for a limit, so we are only interested in large n's and thus we may assume that n > 3 to avoid problems with notation. Then we get

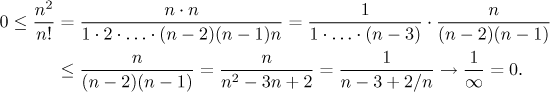
By the second one-sided comparison statement above, the given sequence converges to zero as stated. Note that the last step in the above calculation, the determination of the limit, was done by cancelling n in the fraction. This problem was also typical for the box polynomials and ratios with powers.

Reason 3. Sometimes we do have a reasonable alternative, but we use comparison because it is simples and shorter. For instance, using l'Hopital's rule or the factoring out trick we easily find that

However, comparison does it even faster:

Using comparison proceeds in two steps:

Step 1. Find some comparison(s) (that is, bound(s)) for the given sequence. Oscillating but bounded terms have a natural bound which can be used to derive bounds for the whole sequence algebraically. Often we also get bounds by ignoring parts of the given sequence (see the last example).

Step 2. Find the limit of the bound(s). Then check whether any conclusion is possible by any of the above comparison statements. Remember that the Squeeze theorem requires that both bounds converge to the same limit.

Note: The statements above have a very useful conclusion which can be used as a tool (theorem), it can be stated in several forms.

When a bounded sequence is multiplied by a sequence converging to zero, we get a sequence converging to zero.
When a bounded sequence is divided by a sequence converging to infinity, we get a sequence converging to zero.

Using comparison is less straightforward then the other methods in one crucial aspect: for the other methods we always had typical types for which they were used. Here there is no such type (unless you count oscillating expressions). A lot depends on experience and intuition.

Remark: The two one-sided comparison results in the beginning are very closely related, it is in fact the same problem and the same result. Showing that some sequence converges to infinity is equivalent to showing that its reciprocal converges to zero and vice versa. And when passing to reciprocal, inequalities switch. For instance, in the last example, we can equivalently show that

using the same trick, just turned around:

In Solved Problems - Limits, these methods are used in this problem, this problem, and this problem.

Next box: polynomials, sums and ratios with powers
Back to Methods Survey - Limits