Newtonova metoda

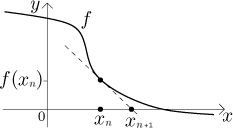
Je dána funkce f (x), hledáme číslo r splňující f (r) = 0. Máme do začátku odhad x_n. Jak dostaneme lepší odhad?

Pokud máme štěstí, pak současný odhad leží na části grafu f, která má jasnou tendenci jít k nějakému kořenu r, například funkce může jít dolů ke kořenu (viz obrázek níže). Jak získáme lepší odhad? Aproximujeme funkci tečnou.

Rovnice tečny je

y = f (x₀) + f ′(x₀)⋅(x − x₀).

Teď potřebujeme získat průnik této přímky s osou x. Rovnice

f (x₀) + f ′(x₀)⋅(x − x₀) = 0

má řešení

x = a_n − f (a_n)/f ′(a_n).

Protože je to náš nejlepší odhad, vezmeme to jako příští odhad, další člen posloupnosti. Tak dostaneme definici

(1)   x_n+1 = x_n − f (x_n)/f ′(x_n).

Jestli chcete vidět pěkný příklad, jak tato metoda selže, koukněte se na tento obrázek:

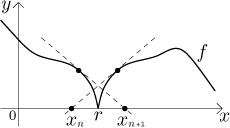
Pokud je "důlek" symetrický, procedura bude stále skákat mezi dvěma naznačenými body, jakoby se houpat ze strany na stranu, a nikdy se nedostane ke kořenu uprostřed. Co je horší, toto není jen divná výjimka, která se prakticky nestane; například funkce

má tuto vlastnost. Ať už zvolíte jakékoliv nenulové x₀, nikdy se Newtonovou metodou nedostanete ke kořenu r = 0.