Newton method

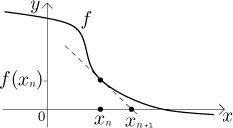
Given the function f (x), we are looking for a number r such that f (r) = 0. We are given some guess x_n. How do we get a better guess?

Well, if we are lucky, the present guess lies on a part of the graph of f that has a definite tendency of going to some root r, for instance the function may be going down towards the root (see picture below). How do we get a better guess? We approximate the function by its tangent line.

The equation of the tangent line is

y = f (x₀) + f ′(x₀)⋅(x − x₀).

Now we need to find the intersection of this line with the x-axis. The equation

f (x₀) + f ′(x₀)⋅(x − x₀) = 0

has the solution

x = a_n − f (a_n)/f ′(a_n).

Since this is out best guess, we take this as the next guess, the next term of the sequence. In this way we get the definition

(1)   x_n+1 = x_n − f (x_n)/f ′(x_n).

To see a nice example of this procedure failing, look at this picture:

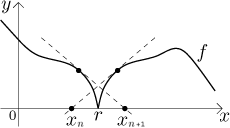
If the "dip" is symmetric, the procedure will just keep changing between the two indicated points, sort of swinging from side to side, without ever getting to the root in the middle. What is worse, this is not something strange that practically does not happen; for instance, the function

has this property. No matter what non-zero x₀ you choose, you will never get to the root r = 0 through the Newton method.