Alternativní definice spojitosti

Jsou dva základní způsoby, jak přistoupit ke spojitosti. Jeden je ten, který jsme použili zde v Math Tutoru, definovali jsme spojitost pomocí pojmu limity. Ja ale také možné definovat spojitost bez použití limity, což je "čistější" z teoretického pohledu. Matematici s teoretičtějím náhledem na věc proto dávají přednost tomuto alternativnímu přístupu a my jej zde ukážeme, protože je možné, že se s tím někteří studenti setkají.

Definice vypadá následovně.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu a. Řekneme, že funkce f je spojitá v a, jestliže pro každé ε > 0 existuje δ > 0 takové, že pro všechna x z D( f ) splňující |x − a| < δ platí | f (x) − f (a)| < ε.

Zkusíme si to přeložit do "normálního" jazyka. Tato definice je v zásadě hra (ona populární hra "epsilon-delta"), podobná té, která se používá při náhledu na pojem limity. My jsme strana, která se snaží ukázat, že daná funkce je spojitá v daném bodě. Náš protivník se nám to snaží zkazit. Dá nám toleranci ε. Naším úkolem je zajistit, že se funkce nehne od hodnoty f (a) o víc než ono dané ε, a nástroj, který máme k dispozici, je omezení grafu f na nějaký kousek okolo daného bodu. Technicky to děláme tak, že specifikujeme, o kolik je povoleno se pohnout doleva či doprava od a, aniž by graf utekl z tolerance; to je to δ. Jinými slovy, máme najít nějaké okolí bodu a, na kterém funkce zůstává v dané toleranci.

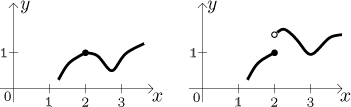
Matematicky, někdo nám dá toleranci ε. My máme najít δ tak, abychom mohli vzít každé x z definičního oboru D( f ) splňující |x − a| < δ a hodnota funkce v x zůstane v mezích dané tolerance od f (a) - matematicky, | f (x) − f (a)| < ε. Pokud to dokážeme, pak jsme vyhráli tuto konkrétní hru; pro spojitost pak musíme být schopni vyhrát všechny možné hry, pro všechny možná epsilon, která nám kdokoliv zadá.

Teď si připomeňme dva příklady ze sekce o spojitosti.

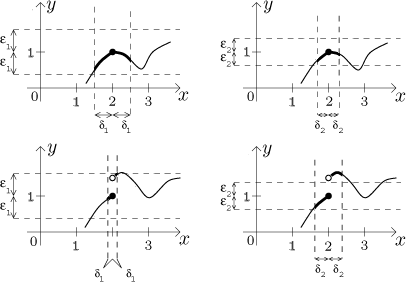
Jak si s nimi tato definice poradí? V následujícím obrázku jsme zkusili pro každou funkci ukázat dvě hry. Pro dva rozdílné epsilony jsme zkusili najít odpovídající delta a části grafu, které tomu odpovídají, jsme zvýraznili. U prvního příkladu (první řada obrázků) se zdá, že ať je nám dáno jakékoliv epsilon, třeba i velice malé, stejně dokážeme najít delta tak, aby odpovídající část grafu ležela v pruhu daném tolerancí epsilon okolo úrovně 1 = f (2), a tak vyhrát hru; to naznačuje, že ona funkce je spojitá v a = 2 podle definice. V druhém řádku jsme se podívali na funkci, která byla napravo, a vidíme, že i když některé hry vyhrát jdou, pro malé epsilony prohrajeme. Ať už zvolíme jakkoli malé okolí okolo a, vždy se v něm najdou body, které po dosazení do f přinutí f vyskočit z dané tolerance. Tato druhá funkce proto podle definice není spojitá v a = 2.

Všimněte si, že obě nerovnosti v definici lze pěkně zapsat pomocí okolí. Podmínka spojitosti pak vypadá mnohem lépe, je to takto: Pro každé ε > 0 existuje δ > 0 takové, že pro všechna x∈U_δ(a) ∩ D( f ) platí f (x)∈U_ε( f (a)). Jak si umíte představit, matematici (kteří si s takovým zápisem tykají), rozhodně dávají přednost tomuto kratšímu zápisu. Dokonce zacházejí ještě dál. Zde je nejobecnější definice spojitosti v bodě a, která funguje pro všechny funkce, nejen pro ty reálné: Pro každé okolí V bodu f (a) musí existovat okolí U bodu a takové, že f (U ∩ D( f ))⊆V.

Podobně definujeme jednostrannou spojitost, jen musíme omezit x na příslušnou stranu od a.

Definice.
Nechť f je funkce definovaná na nějakém levém okolí bodu a. Řekneme, že funkce f je spojitá zleva v a, jestliže pro každé ε > 0 existuje δ > 0 takové, že pro všechna x z D( f ) splňující a − δ < x ≤ a platí | f (x) − f (a)| < ε.
Nechť f je funkce definovaná na nějakém pravém okolí bodu a. Řekneme, že funkce f je spojitá zprava v a, jestliže pro každé ε > 0 existuje δ > 0 takové, že pro všechna x z D( f ) splňující a ≤ x < a + δ platí | f (x) − f (a)| < ε.

Definice spojitosti, zejména její podstata coby hry, vám měla připomenout definici limity. Vlastně je skoro stejná. Jediný rozdíl v mantře "pro každé... existuje..." je v tom, že při definici limity jsme nedovolili x, aby se rovnalo a, zatímco u spojitosti je i a zahrnuto do hry. Z toho odvodíme následující fakt:

Věta.
Uvažujme funkci f. Tato funkce je spojitá v a zleva tehdy a jen tehdy, jestliže má limitu v a zleva a tato limita je rovna f (a).
Tato funkce je spojitá v a zprava tehdy a jen tehdy, jestliže má limitu v a zprava a tato limita je rovna f (a).
Tato funkce je spojitá v a tehdy a jen tehdy, jestliže má limitu v a a tato limita je rovna f (a).

To ukazuje, že alternativní definice spojitosti definuje stejný pojem jako definice z naší sekce o spojitosti.

Tato věta by také měla vypadat přirozeně. Když jsme kdysi dávno nahoře začínali se spojitostí, řekli jsme si, že vlastně jde o to, jestli graf f jde do určitého bodu, jak se x přibližuje k a, a tato formulace už měla ledacos připomenout. Pokud si připomenete definici limity a znovu přečtete ten úvod nahoře, mělo by to všechno být jasné.