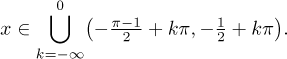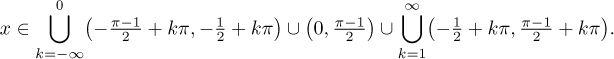Zde vyřešíme nerovnost dělením pomocí x, musíme rozlišit dva případy:
a) x > 0. Pak prostě vydělíme a dostaneme
sin(2x + 1) > 0. To se dá vyřešit například tak, že si představíme graf
sin(y).

Vidíme, že sin(y) je kladný přesně tehdy, je-li y z
intervalu (0,π) a jeho
posunů o 2kπ pro
libovolné celé číslo k. V našem případě to znamená, že výraz
2x + 1 musí náležet do jednoho z intervalů
(2kπ,π + 2kπ).
Můžeme to přepsat jako nerovnost (či přesněji řečeno dvě)
2kπ < 2x + 1 < π + 2kπ,
vyřešíme je pro x (lze řešit obě najednou) a dostaneme
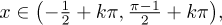
kde k je libovolné celé číslo.
Teď si ale musíme připomenout, že toto řešení jsme dělali za předpokladu, že
x > 0, takže můžeme vzít jen tu část řešení, která zahrnuje
kladná čísla. Jestliže k > 1; pak odpovídající intervaly leží na
kladné části osy x a přežijí. Pro
k < 0 obsahují odpovídající
intervaly pouze záporná čísla a lze je tedy ignorovat. Pokud
k = 0,
dostaneme interval (−1/2,π/2 − 1/2), jehož část leží v
kladných číslech, tak bereme pouze onu část. Dostaneme tedy

b) x < 0. Když teď vydělíme nerovnost, musíme prohodit směr
nerovnosti, dostaneme tedy
sin(2x + 1) < 0. Podobně jako předtím
odhadneme z grafu sinu, že 2x + 1 musí náležet do intervalů
(−π + 2kπ,2kπ).
Když se na to podíváme jako na nerovnosti
-π + 2kπ < 2x + 1 < 2kπ
a vyřešíme, dostaneme
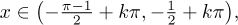
kde k je libovolné celé číslo.
Jako předtím si musíme připomenout, že jsme toto řešení dělali za
předpokladu, že x < 0, takže můžeme vzít jen tu část řešení, která
obsahuje záporná čísla. Dostaneme tedy
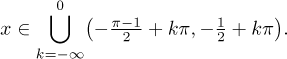
c) Abychom pokryli všechny možnosti, musíme ověřit, co se stane, když
x = 0, a hned vidíme, že to není řešení dané nerovnosti,
takže tato část k řešení nic nepřidá.
Protože jsme měli na výběr mezi třemi alternativami, konečné řešení dostaneme
sjednocením částečných řešení:
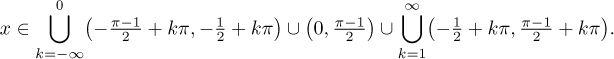


![]()

![]()