Nejprve se podíváme na řešení faktorizací a určením znamének. K tomu se dostaneme tak, že budeme řešit každou rovnici zvlášť a upravíme si je do tvaru s 0 na jedné straně.
Levou nerovnost jde upravit na
![]()
Nerovnost lze vydělit trojkou, takže vidíme, že stačí určit znaménko výrazu na pravé straně a podívat se, zda je kladné (nebo nula). Dělící body jsou 3 a 9, takže dostaneme tuto tabulku:

Teď vidíme intervaly, kde je zlomek kladný, dosazením dělících bodů také vidíme, že 9 nedává smysl, takže jde ven, ale 3 dává 0, což splňuje danou nerovnost a proto bude 3 zahrnuto. Závěr tedy je, že levá nerovnost má řešení
Teď se podíváme na pravou nerovnost:
![]()
Zpracujeme ji přesně jako tu levou:

Řešení je
Teď musíme obě části spojit. Protože obě nerovnosti mají platit současně, vezmeme průnik částečných řešení, proto řešení dvojité nerovnosti je
Alternativní řešení:
Teď zkusíme začít tím, že se zbavíme zlomku, což se udělá tak, že se řetězec
nerovností vynásobí členem

Na každé půlce reálné osy teď řešíme dvě nerovnosti, ale ty jsou velice snadné. Protože chceme, aby tyto nerovnosti platily současně, ona dvě řešení budeme protínat, a ten výsledek pak ještě protneme s oblastí, na které jsme řešili.
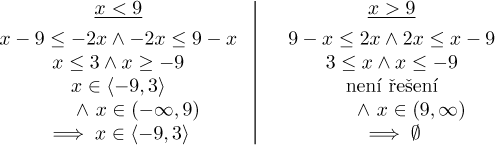
Protože máme svobodu výběru, jaké x zkusit, zda