Deciding 1-1, finding an inverse of a real function: Survey of methods

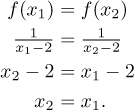
There are two basic methods for deciding whether a function f is 1-1.

By definition. Start with the equation f (x₁) = f (x₂). It has one trivial solution x₁ = x₂, the point is to check whether there is also another solution, when x₁ and x₂ are distinct. If there is, then the function is not 1-1. If the trivial solution is the only one, then the function is 1-1.

Using theory. There are several theorems that guarantee that a function is 1-1. Probably the easiest and at the same time very useful is this:

If a function is strictly monotone on a set, then it must be 1-1.

In particular, if a function is continuous on an interval I, differentiable on its interior, the derivative is never zero and has the same sign on this interior, then the function is 1-1 on I.

Inverse function

Once we have a function that is 1-1 somewhere, we can find its inverse by solving the equation y = f (x) for x, we get x = f₋₁( y).

Example: Decide whether the function f (x) = 1/(x − 2) is 1-1, if it is so then find its inverse.

Solution: First we will show that this function is 1-1. Since it looks simple, we try it by definition.

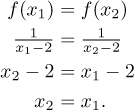
Since all the steps were equivalent, there is really only the one solution and the function is therefore 1-1.

Note that if we tried the theory way, we would have a problem. The domain of this function is D( f ) = (−∞,2) ∪ (2,∞). On each interval, the derivative −1/(x − 2)² is negative, therefore the function is decreasing, hence also 1-1. Unfortunately, having function that is 1-1 on two intervals does not allow us to make any conclusion about f on the union of these intervals, since it may well have the same values on these two intervals. In fact this is not the case here, but this shows that the approach via monotonicity works well only on individual intervals, on more complicated sets we either have to go by definition or do some more work, for instance sketch the graph.

Anyway, we have a function that is 1-1 on its domain and now we want to find its inverse:

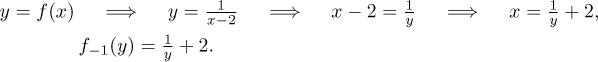
If we wanted to work just with the inverse function without relation to the original f, we would not need to be reminded of the setup by the variable y, it could be more convenient to relabel the variable to the usual x:

Important properties:
1. The domain and range exchange places:

D( f₋₁) = R( f ),     R( f₋₁) = D( f )

2. The graph of the inverse function can be obtained by taking the graph of f and flipping it around the main diagonal y = x. Note that if it is done properly, then the monotonicity of f and its inverse agree. Precisely, if a part of a graph (on an interval) is increasing, then after flipping this piece must also be increasing; the same works for decreasing.

Example: On the left we show the graph of some 1-1 function f, on the right its inverse.

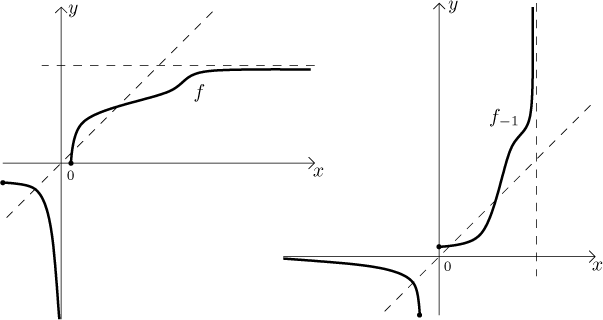
For more examples see Solved problems.

Transformations, graph guessing
Back to Methods Survey - Basic properties of real functions