Problem: Determine whether the following function is 1-1, and if yes then find its inverse function. Also investigate monotonicity.

Solution: First note that the domain of f is all real numbers apart from −1.

To determine injectivity we use the standard approach. We take x1, x2 from the domain, assume that they give the same value when substituted into f and we check whether there is some other solution besides the trivial one.

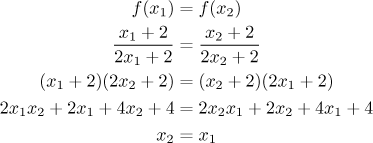
We see that the only way to get the same value is to start from the same place, which shows that the function is 1-1.

Now we find the inverse function by solving the equation y = f (x) for x:

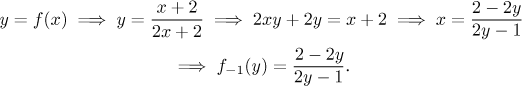
Now we need to investigate monotonicity. So far we know only the definition, so we will try to establish one of the two necessary implications. We take arbitrary two numbers x1 < x2 from the domain and we will try to conclude that f (x1) < f (x2), which would give that f is increasing, or that always f (x1) > f (x2), which would give that f is decreasing; it is also possible that none of this is possible, then there is most likely some problem with monotonicity.

How do we establish those implications? We start with the inequality x1 < x2 and try to use equivalent operations to create the expression for f on both sides. Unfortunately, here we run into a problem right away, since in the formula for f the variable x appears at two places and we do not have equivalent transformations that would somehow bring more appearances of one variable to an inequality.

Fortunately, the given function is a ratio of linear functions, for which we have a very handy favourite trick: We divide with remainder. In fact, for this particular case there isan alternative for the usual algorithm for long division. Namely, we create the expression in the denominator also on the top, first we create the appropriate number of x on the top by multiplying/dividing, then we use addition/substraction to also fix the absolute term. We will write all details, with a bit of experience this can be done very quickly.

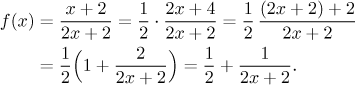
This kind of expression we may try to create, we always start from x in this expression and keep going out in the order of evaluation. First we multiply both sides by 2, then add 2.

The next step is to move the linear terms into denominators on the opposite sides of the inequality. This is done by dividing the whole inequality by the appropriate term, but here we have a big problem. When dividing an inequality, the sign of the number that we divide with determines whether we should switch the direction of inequality or not. Here we do not know, so as usual we will look at all possibilities. 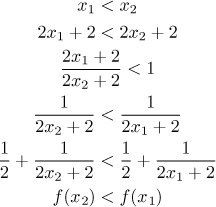We start by assuming that x1 > −1, then also x2 > −1 since it is greater. With this choice, both terms (2x + 2) in the inequality are positive.

We divided first by (2x2 + 2), then by (2x1 + 2), at the end we added 1/2 to both sides. Thus we established one of the implications we were interested in, but note that only assuming that the variables are > −1. Fortunately for us, this can be rewritten in the form that these variables belong to a certain set, namely the interval (−1,∞). Thus we proved that for all couples x1 < x2 from (−1,∞), the order gets reversed when the function is applied (larger argument leads to smaller function value), that is, we just proved that f is decreasing on the interval (−1,∞).

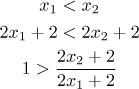
Now we have to look at the other alternative, when x1 < −1. When we divide by the corresponding term, we have to switch the direction of inequality, since the term is negative.

In the next step we would like to divide by (2x2 + 2), but unlike the first case, here we do not have the relevant info about x2, since this time it does not follow from x1 < −1.

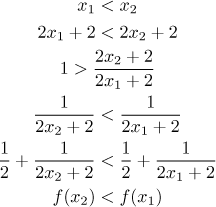
The "good" case is when also x2 < −1. Assuming this we can finish the procedure, again we have to switch the direction when dividing.

Just as before, the direction in comparison was reversed and the condition "x1 < −1 and x2 < −1" is of the interval type, so in fact we have just proved that f is decreasing on the interval (−∞,−1).

Right now we can conclude that f is decreasing on (−∞,−1) and on (−1,∞). If the question was "identify itnervals of monotonicity" then we would be done, because nothing more in this direction is possible: These two sets give the domain and cannot be connected into one interval. In most applications this analysis would be sufficient.

But we were asked to investigate, so perhaps more is expected. Can we put the two sets together into one set (not an interval) and say that the function is decreasing or perhaps non-increasing on its domain? (Given monotonicity on the two subintervals, no other monotonicity is possible now.) Right now we do not know, so we need to do more work.

Which brings us to the last case for variables, when x1 < −1 and x2 > −1:

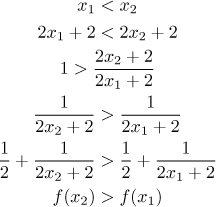
This time we obtained an implication that suggests increase, which does not sound good. We claim that our function is not monotone on its domain. It cannot be increasing or non-decreasing because of it behaviour on the two intervals. Possibility of being decteasing or non-increasing is ruled out by the latest calculation. Indeed, we can choose, say, x1 = −2 and x2 = −2, then x1 < x2, but we easily confirm that f (x1) > f (x2).

Note that strict monotonicity implies injectivity, from the decreasing parts we therefore know that f is 1-1 on (−∞,−1) and also on (−1,∞), but we know that intervals of injectivity cannot be connected into larger sets without further investigation.

Note also that the "divided" form of the ratio of linear functions makes also other calculatios easier. We briefly return to the first two topics. First we check that this function is 1-1:

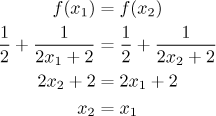
Now we find the inverse function.

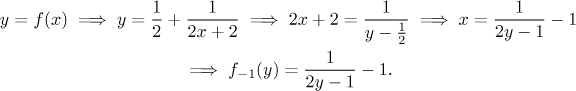
It is easy to check that we got the same answer.

Next problem
Back to Solved Problems - Real functions