Problem: Determine whether the following function is 1-1, and if yes then find its inverse function. Also investigate monotonicity.

Solution: The domain of this function is the whole real line. We decide injectivity by taking the equation f (x₁) = f (x₂) and checking whether there is other solution than the trivial.

Well, that's the end of the road, we have absolutely no idea what to do with this algebraically.

Our only hope comes from the theory. Can we say something about monotonicity of this function? This is actually another part of this question, so we do it here right away. To investigate monotonicity by definition, we have to start with a couple x₁ < x₂ from the domain and try to apply operations to this inequality to create the given function on both sides. Here it does not look as simple as in the previous problems, since the variable appears at three places in the function and inequality manipulations do not allow to add more x's. Fortunately for us, here we have addition of terms and inequalities can be added assuming that they go in the same direction.

Thus we can start with the basic inequality x₁ < x₂ and apply the cube power to it, which we can do (and without changing the direction in the inequality) as the cube power is increasing. In words, it changes smaller numbers into smaller cubes, larger numbers into larger cubes, so the inequality survives. For similar reasons we can also apply the 5th power to the initial inequalitym then we add them:

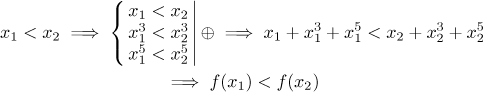
We just proved that for any two numbers from the domain, the function preserves their order, so the given function is increasing on its domain.

Note: Here it might be easier to use our favourite method for determining monotonicity and check on the derivative:

Since the derivative is always positive on the interval ℝ, the function is increasing on this set (see Derivatives - Theory - MVT).

Back to the initial question. Since the function is strictly monotone on its domain, it is also 1-1.

To find the inverse we solve the equation y = f (x) for x.

It's over, we have no idea what to do. We know that the inverse function exists, but we are unable to find it.

Next problem
Back to Solved Problems - Real functions