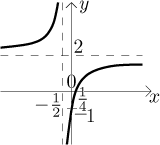
Problem: Using the knowledge of transformations guess the graph of the following function:

Solution: First we need to identify the basic function whose shape we start with. However, this is not possible here, since the variable x is here twice. The guessing procedure always starts from some elementary function and in all of then the variable appears only once, transformations then do not allow to multiply its presence.

Fortunately for us, in this particular example there is a way out. We have a ratio of linear functions and this expression is usually much more user-friendly when divided with remainder, we actually use our favorite trick instead and create the denominator in the numerator. First we fix the correct quantity of x by multiplying/dividing, then we fix the absolute term by adding/substracting.

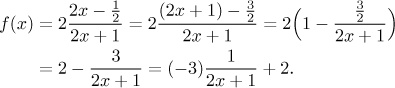
We made the very last step to prepare the expression for analysis. Now we have just one x and we are ready to identify the basic function. First, we know that the expression in the denominator can be created using shift and scaling, so we can disregard it and only consider (−3)⋅1/x + 2. Again, scaling by (−3) and shift by 2 can be disregarded, this time they are applied to the function 1/x, which is our basic function.

So we start with the graph of the function 1/x and first transform its argument. There are two transformations, scaling by 2 and shift by 1. They are calculated in this particular order and the rule for argument says "last to first", so we should first do the shift by 1 to the left and then scale the function, we will be shrinking it twice in the orizontal direction (towards the y-axis). We check that this order really creates what it should by replacement notation:

x → x + 1 → (2x) + 1.

In each step we replaced x itself by the corresponding transformed expression and obtained what we need, so the order is correct. Let's do it.

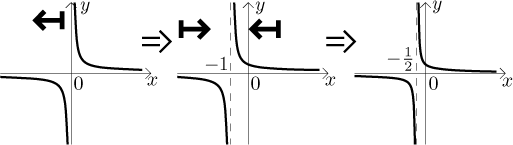
Quick check that we did not make any major mistake so far: There is a hole in the domain at −1/2, which seems to fit with our picture.

Now it is time to apply transformations to the value. There are two, scaling by (−3) and shift by 2, they are evaluated in this order. The rule for value says "first to last", so the transformations should be applied in the same order. First scaling, we will stretch the function vertically, away from the x-axis, 3 times, and because of the negative sign we will also flip the picture about the x-axis. Then we shift the resulting picture up by 2.

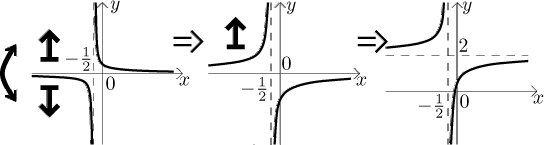
That should be it. However, we recommend that two more things be done.

First, we check that the graph we guessed is not completely off by calculating major features. There are two very prominent features, the vertical and horizontal asymptote. The vertical asymptote is at the hole in the domain −1/2, so our picture got it right, and when we calculate one-sided limits at −1/2 (experienced student can do it mentally, without writing anything), we see that also the directions at which the graph runs away are correct, it goes to infinity on the left and negative infinity on the right from −1/2.

Then we look at the limit of the function at infinity and negative infinity and obtain 2 (again, this is easy just by looking at the expression), so we got the horizontal asymptote right as well. We can now be quite confident that we guessed it well.

Now the second thing. The guessing procedure is quite reliable in the hands of an experienced student, so if we have a nice and correct graph, it might be worthwile to made little adjustments to the graph to also capture further information correctly. There are two very prominent points, the intercepts. So we calculate the y-intercept: f (0) = −1, and the x-intercept: f (x) = 0 gives x = 1/4. We adjust the graph accordingly and add labels, now we have a very respectable looking graph.

Next problem
Back to Solved Problems - Real functions