As it happens so often, there are two schools in defining continuity. We required here that a function be defined on some neighborhood of the a that we investigate, because if f does not exist around a, then it seems pointless to ask whether the graph approaches the appropriate point well - there is no graph around! So the definition that we have here seems reasonable and for elementary calculus it seems more suitable. However, some people prefer to drop this assumption, they would happily ask about continuity even if f does not exist around a. In fact, this definition has a good justification, too, since then it agrees with the general definition of continuity for mappings and mathematicians prefer to have things neat.
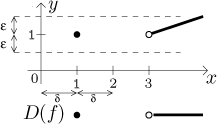
After some hard soul searching (after all, the author is a research mathematician himself) we decided to adopt the definition above, since Math Tutor is definitely not for scientistc but for ordinary humans trying to pass their calculus course. In most cases the two definitions give the same answers, and the few minor differencies usually do not cause much trouble. Still, check what definition your prof uses and be careful. Just to show an example of this difference, consider the following function.

By our definition, we would ask about continuity at a for
People who prefer the alternative definition would also ask about continuity
at