
Nejpopulárnější jednotka pro měření úhlu je stupeň. Máme 360 stupňů v plném kruhu, 90 stupňů je pravý úhel. Jsou v zásadě dva způsoby, jak specifikovat úhel mezi dvěma paprsky.
1. Pokud jsou paprsky stejně důležité, dostaneme neorientovaný úhel (například mezi stranami trojúhelníka). Jsou-li dány dva paprsky, vždy bereme ten menší úhel, změříme jej a vyjádříme odpověď jako kladné číslo (nebo nula).

2. Pokud je jeden paprsek určitým způsobem speciální (například osa x souřadnicového systému), pak obvykle používáme orientovaný úhel, braný kladně proti směru hodinových ručiček (směrem k ose y) a záporně ve směru hodinových ručiček.
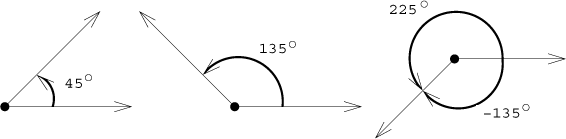
Vidíme, že tentýž úhel lze specifikovat několika způsoby, dokonce nekonečně mnoha způsoby, protože v této situaci můžeme obejít počátek dokola několikrát, pokaždé přibude plný kruh (360 stupňů) a můžeme jít i opačným směrem.
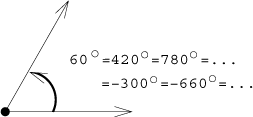
Stupně jsou "praktické". Lidé je používají při práci s geometrickými objekty, počítání vzdáleností a úhlů "ve skutečném světě" a v podobných situacích. Protože odpovídají směrům na kompasu, dobře si s nimi rozumíme. V těchto situacích také často používáme neorientovaný úhel.
Na druhou stranu ve vědách, hlavně v matematice, (téměř) vždy používáme orientovaný úhel a dáváme přednost jiné jednotce: radiánu.
Je-li dán úhel, dostaneme jeho velikost v radiánech tak, že vydělíme délku oblouky poloměrem.
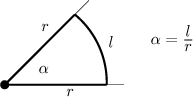
To je jedna z velkých výhod radiánu, protože v situacích jako na obrázku
hravě spočítáme délku oblouku coby
Plný úhel je (obvod)/(poloměr), tedy plný úhel je
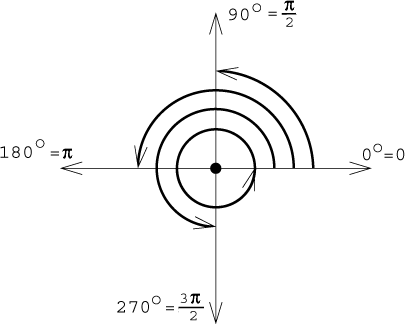
Vztah mezi stupni a radiány je lineární, takže máme jednoduché transformační vzorce:
![]()
Asi nejpopulárnější úhly jsou tyto:
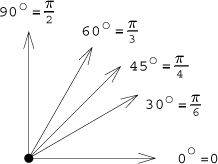
Proč jsou populární?
Poznamenejme, že když uvažujeme pravoúhlý trojúhelník s dalším úhlem
Přičítáním/odečítáním pravých úhlů dostaneme celou "růžici kompasu":
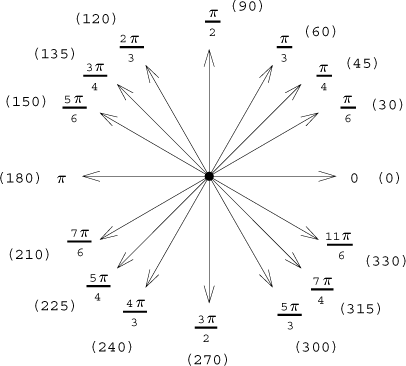
Protože jsou tyto dvě jednotky svázány lineárně, můžeme je pro měření
používat obě bez nějakých problémů. Věci se ale změní, když tato měření
použijeme ve výpočtech. Obzvláště opatrní musíme být, když dosazujeme úhly do
goniometrických funkcí. Tabulky řekněme sinu jsou rozdílné pro úhly měřené ve
stupních a úhly měřené v radiánech. Například pokud máme sinus, který očekává
radiány, dostaneme
Pro 90 stupňů potřebujeme jiný sinus, takový, který očekává stupně. Toto je ostatně docela populární zdroj chyb ve výpočtech, když student zapne přepnout kalkulačku na stupně (či radiány, cokoliv je zrovna potřeba).
Proto jsou "sinus ve stupních" a "sinus v radiánech" dvě zcela rozdílné
funkce. V matematice, fyzice a dalších vědách potřebujeme přesné specifikace,
a tak bylo už dávno rozhodnuto držet se radiánů. Jak jsme poznamenali,
radiány jsou lepší pro vědecké výpočty, takže to má smysl, a navíc to dává
pěknější vzorce, například pro derivaci máme
Abychom to shrnuli, pamatujte, že v kalkulu žerou všechny goniometrické funkce zásadně radiány.