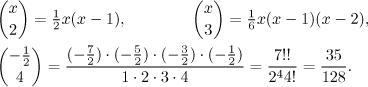Factorial is not really a real function (see later), but it is so important that we include it here among useful functions.
Definition.
Let k be a positive integer. We define the factorial of k as
k!=1⋅2⋅3⋅...⋅(k − 1)⋅k. We also define
0! = 1.
Examples:
Factorial grows very quickly, for instance
An important property of factorials is that they readily cancel in fractions. For instance:
![]()
Similarly
![]()
The down side is that there are no nice algebraic properties, for instance
there are no nice formulas for things like
Such expressions cause mistakes when factoring, here is one correct example:
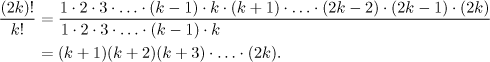
Nothing more can be done with it.
There is a thing called double factorial, where instead of multiplying all numbers one takes just every second.
Definition.
Let k be a positive integer. We define k!! as
k!! = 1⋅3⋅5⋅...⋅(k − 2)⋅k for k odd,
k!! = 2⋅4⋅6⋅...⋅(k − 2)⋅k for k even.
Examples:
Factorial is a function whose domain is natural numbers and zero. Is it possible to extent this definition to a larger set (like to all non-negative real numbers) by somehow connecting the dots in the graph? This would be very helpful, for instance it would allow us to use the l'Hospital rule when calculating limits with factorials. The good new is that the answer is yes, there is a function defined on all real numbers apart from negative integers which agrees with factorial at natural numbers, see the Gamma function. The bad news is that this function is not exactly easy to work with and in particular, the tricks for limits that we covered are much better in dealing with factorials than messing around with Gamma functions.
Definition.
Let n ≥ k be non-negative integers. We define
This is called the binomial coefficient, also binomial number, or combinatorial number. We read this expression "n choose k".
Example:
![]()
Some identities:
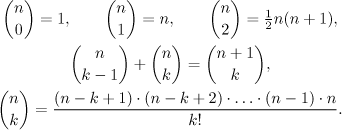
The last identity is very interesting, since on the right there are no factorials on the top, that is, the variable n is free to change. Thus we can introduce a useful generalization.
Definition.
Let x be a real number, k a natural number. We define the binomial number by
Examples: