sin(1/x) and relatives

This section is actually a companion to the previous section, "saw-like" functions. We will show functions that exhibit similar behaviour as some of the examples there, but they will be "smooth", that is, all the examples will be differentiable as many times as we want away from x = 0.

Example 1

Consider the following function:

What can we say about this function? We know that it oscillates between −1 and 1. Its zero points are 1/(kπ), note that these form a sequence that tends to 0. Since the waves of sine are between these zero points, it follows that the waves are getting denser and denser towards the origin, the graph looks like this:

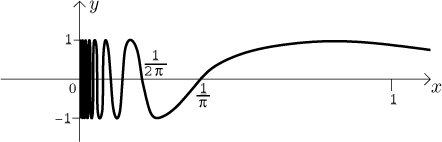
Note that there are infinitely many waves, the function never stops oscillating between −1 and 1 as we approach the origin, so it follows that there is no limit at 0 from the right. On the other hand, for x > 0 the function has all derivatives.

Example 2

Consider the following function:

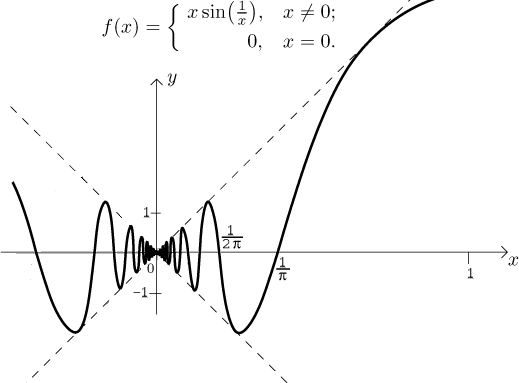
Here we still have the never ending oscillation around the origin, but now its amplitude is modified by the term x, so it follows that this function has limit 0 at x = 0. Since this agrees with the definition at 0, this function is continuous at the origin. Consequently, this function is continuous everywhere, and for non-zero x it also has all derivatives. However, we do not have a derivative at 0. Reasoning for this conclusion is similar as we saw in the section on "saw-like" functions; when we construct the lines approximating the tangent line and go to the origin, the slopes change between −1 and 1 and never settle down. Conclusion:

Example 3

Consider the following function:

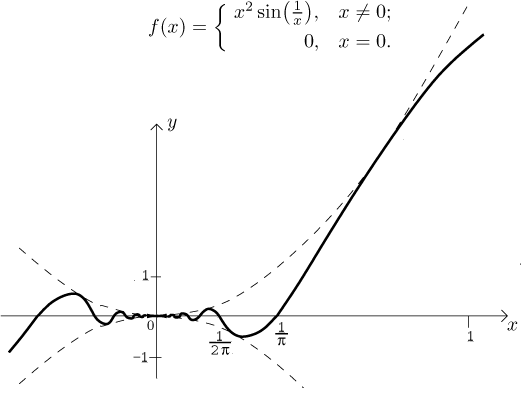
Again, here we have a function that is continuous everywhere and differentiable as many times as we want at non-zero points. But this time we also have a derivative at the origin, and again, reasoning is similar to that concerning the corresponding function from "saw-like" functions, but here we can actually calculate the derivative at zero quite easily using definition. Thus we have

Convince yourself by calculating the appropriate limit that this first derivative is not continuous at the origin. This shows that there exist functions that are differentiable everywhere but the resulting derivative is not continuous (cf. Derivative: basic properties in Derivatives - Theory - Introduction). However, this derivative does have the Intermediate Value Property.

Just like in the previous example we can prove that the second derivative of this function does not exist at the origin. In general, we can fix a natural number n and consider the following function:

This function is continuous on the real line, it has all derivatives at non-zero x and it has derivative at x = 0 equal to zero up to the order (n − 1), but it does not have the n-th derivative at the origin.

Dirichlet function
Back to Theory - Elementary functions