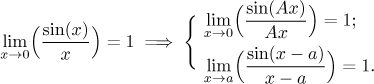
This is a method that helps with evaluating some limits. It can be viewed as a simple smart trick or one can create a story about it, which brings us to the name. The word "infinitesimal" definitely does not refer to the infinitesimal dx as we know it from differentiability or continuity according to Leibniz. The meaning is different and we will explain below. First let's see the simple way.
The following limit is quite well-known, and using substitution we easily derive other versions:
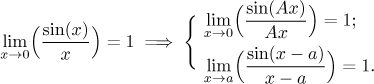
We can use these to simplify other limits as follows (we show the process in detail to justify it):
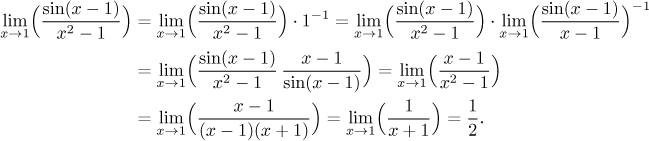
Compare the first limit and the last on the second line. We esentially
replaced the sine with
Theorem.
Let a be a real number, ∞, or−∞. Let f, g, h be functions defined on some reduced neighborhood of a. If
then
Note that we already discussed the situation when the ratio of two functions
f and h converges to 1 at a in the section on
order of functions and
introduced the following notation:
• If
Note the restriction on the type of expression. In general we cannot replace just anywhere, as we will discuss below.
We often evaluate limits at
Here is a list of the most popular equivalent infinitesimals.
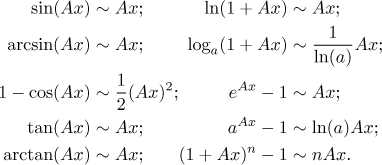
Note that the n in the last formula can be any positive real number, for instance a fraction. The formula thus helps also with roots.
Example: We will solve the following limit using equivalent infinitesimals.
![]()
This was significantly easier than using l'Hospital's rule. However, one can use it at school (at an exam) only if equivalent infinitesimals were properly established in class.
The above formulas can also help with limits at other points than 0 using suitable substitutions.
Example:
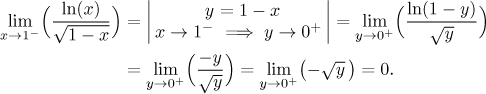
Example:
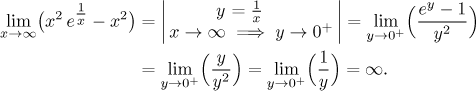
The main limitation of this method is that we can safely replace only a denominator or numerator as a whole. Indeed, consider the following example.
Example:
![]()
This result is wrong, the correct answer is
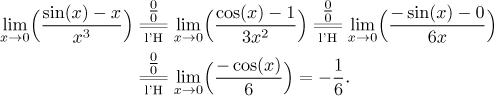
Looking at the table of equivalent infinitesimals above, one can notice that in all cases the term on the right is in fact the first term of the Taylor expansion of the function on the left. This is no accident. In general, when evaluating a limit at a, we can replace functions by their expansions with center a. If we use the full expansion (power series), we can do it as we wish assuming that the power series converges the original function on some neighborhood of a.
However, working with a series may be difficult. Often it is better to use just a non-zero Taylor polynomial of a certain degree. Then we have to be careful not to make a mistake. We can definitely do this if the function we want to replace is exactly the numerator or denominator in a fraction that we are investigating. If we want to replace in other places, then we have to choose the degree in such a way that we do not loose crucial information. Intuitively, we can replace a part of the investigated expression with its Taylor expansion of a certain degree in situations when the replacement does not get entirely cancelled in the process. This is not exactly a proper mathematical statement, it would be difficult to give a complete and precise description given how diverse limit problems can be. When you decide to use replacement, a lot of experience and good understanding are necessary.
As an example we return to the calculation above that did not work out. We will show it twice.
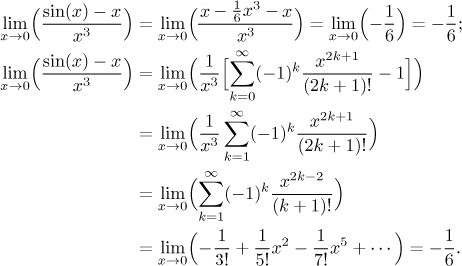
Since equivalent infinitesimals are not commonly taught, we will not use them in official solutions here in Math Tutor. We start by observing that when we replaced the sine with first degree polynomial, it got cancelled. Thus it was too short. We try the next available length, that is, the third degree polynomial, because a part of it should survive in the numerator.