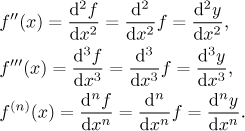
Higher order derivative, total differential

Higher order derivatives is actually a pretty simple idea. When we take a derivative of a function, we get the first order derivative, derivative of order 1, or just the first derivative. To get the second derivative, we differentiate once more (if possible), so f ′′ = [ f ′]′. Similarly, by taking the derivative three times we get the third derivative etc. In general we have to use induction to define the n^th derivative. Where do we start? It is convenient to start with the 0^th derivative, which is just f, we differentiate zero times, that is, not at all. Finally, we need to decide on notation, since it wouldn't be convenient to denote, say, the 23^rd derivative using apostrophes, we also would not be able to denote a general order derivative. The standard notation for the n^th derivative is f ⁽ⁿ⁾ (note the parentheses).

Definition.
Consider a function f defined on a neighborhood of a point a. We define the 0^th derivative, or the derivative of order 0, as f ⁽⁰⁾(a) = f (a).
For n a natural number we define the n^th derivative, or the derivative of order n at a by induction as f ⁽ⁿ⁾(a) = [ f ⁽ⁿ⁻¹⁾]′(a) if it exist.

If the n^th derivative at a exists, we say that f is n-times differentiable at a.

Let f be a function on an open set G. If its n^th derivative exists at all points of G, we say that f is n-times differentiable on G.

Example: We will find all derivatives of f = x³ − 5x² + 13.
f ⁽⁰⁾ = f  = x³ − 5x² + 13.
f ⁽¹⁾ = f ′ = [x³ − 5x² + 13]′ = 3x² − 10x.
f ⁽²⁾ = f ′′ = [ f ′]′ = [3x² − 10x]′ = 6x − 10.
f ⁽³⁾ = f ′′′ = [ f ′′]′ = [6x − 10]′ = 6.
f ⁽⁴⁾ = f ′′′′ = [ f ′′′]′ = [6]′ = 0.
f ⁽⁵⁾ = f ′′′′′ = [ f ′′′′]′ = [0]′ = 0.
Obviously, f ⁽ⁿ⁾ = 0 for all n > 3. This function f is infinitely many times differentiable on the real line.

Alternative notation:
When writing derivatives, people usually do not write the apostrophes "properly", with the little dot and a curved tail, rather they just make dashes. A dash can also be interpreted as an upper-case I. This inspired another notation that is used for derivatives of higher order, namely with Roman numerals. Derivatives up to the third one are written normally, but then we can write f ′′′′ = f ^IV, f ′′′′′ = f ^V, the 6^th derivative is f ^VI, the 7^th derivative is f ^VII, etc.

Higher derivative and other notations:
The Leibniz notation:

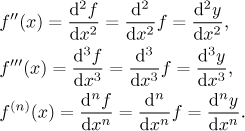
The dot notation (we use function x with variable t):

The subscript notation:

Total differential is a notion that comes out of the desire to approximate a given function f by a linear function close to a given point a. When the function has just one variable (which is our case), then also the linear function has one variable and describes a line. The best fitting line is the tangent line, so in one variable the total differential is just another guise for the tangent line. Thus it does not really bring anything new, but we include it here for the sake of completeness.

Definition.
Consider a function f defined on a neighborhood of a point a. By a total differential of f at a we mean a linear transformation L(h) that satisfies

Notation: The total differential of f at a is denoted by df (a), so when we substitute h, we write it as df (a)[h].

The definition means the following. Assume that we have a total differential at a. If x is very close to a, then f (x) should be almost f (a) + L(x − a). We have the following theorem.

Theorem.
Consider a function f defined on a neighborhood of a point a. There exists a total differential of f at a if and only if f is differentiable at a. Then also

df (a)[h] = f ′(a)h.

So indeed, in one dimension the total differential is just the idea of derivative written in a different way. This is even more obvious when we write the total differential in an alternative way (which is actually quite common), using the differential dx in place of h:

df (a)[dx] = f ′(a)dx.

Equally common shortcut that gives the total differential at all points a (that is, on a set) is

df = f ′dx.

We had an equation just like this in the section on Leibniz notation. Why do we then bother with the total differential? When we start considering functions of more variables, that is, functions that live in more dimensional spaces, then there is no obvious way to generalize the notion of derivative so that it carries all the properties we love in one dimension. However, the notion of the total differential can be easily generalized and turns out to be rather useful, it can be even used in more abstract spaces.

In fact, we have the general definition above already, since we can use the statement as we have it with just one change in the basic setup. Instead of real numbers as the space where f lives we take a reasonable abstract space S, which above all means that in this space we have some linear operations and the notion of neighborhoods of points. Using these neighborhoods we can define the notion of a limit exactly as we did with real numbers. The definition of total differential, where we now take a and h from the space S, now makes sense. Of course, this all is way beyond the level of Math Tutor.

Derivative and operations
Back to Theory - Derivative