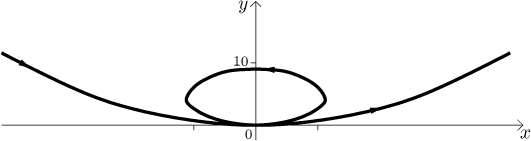
Příklad: Načrtněte graf parametrické křivky dané
x(t) = t³ − 9t,
y(t) = (1/9)t⁴ − 2t² + 9   pro reálná t.

Řešení: Nejprve se podíváme na základní věci. Jak najdeme průsečíky s osami?

Průsečík s osou x najdeme vyřešením rovnice y(t) = 0.

Existují dvě hodnoty parametru, pro které křivka protne osu x, jmenovitě t = −3 a t = 3. Dosadíme tyto hodnoty do x, abychom tyto průniky našli jako body v rovině: x(−3) = 0 = x(3). Pro ony dvě hodnoty parametru tedy křivka vlastně prochází počátkem.

Průniky s osou y najdeme vyřešením rovnice x(t) = 0.

Jsou tři hodnoty parametru, při kterých křivka protíná osu y. Hodnoty t = −3 a t = 3 už jsme probrali výše, teď také máme t = 0. Dosadíme do y: y(0) = 9. Když je tedy parametr t = 0, pak křivka prochází bodem (0,9) v rovině.

Další zajímavá otázka je, co se stane "na koncích". Nejprve se podíváme na parametr poblíž mínus nekonečna:

To znamená, že když pošleme parametr do mínus nekonečna, tak křivka jde směrem k "hornímu levému rohu" roviny. Teď se podíváme na opačný "konec" křivky.

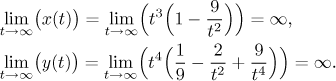
To znamená, že když pošleme parametr do nekonečna, tak křivka jde směrem k "pravému hornímu rohu" roviny. Zatím tedy víme toto:

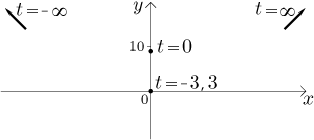
Bonusový fakt: Všiměte si, že y(t) je funkce sudá, zatímco x(t) je lichá funkce. To znamená, že výsledná křivka je symetrická vzhledem k ose y.

Teď se podíváme na směry, kterými tato křivka jde pro různé hodnoty parametru. Víme, že body, kde se směr mění, jsou právě kritické body funkcí x a y. Jsou dva druhy kritických bodů. Dostaneme je, když derivace neexistuje, ale to se pro naše dvě funkce nestává. Další kritické body jsou ty, kde je derivace nulová.

Máme pět kritických bodů, které reálnou osu (coby místo, kde žije parametr), rozdělí na šest sekcí. Na každém z těchto úseků jsou x i y monotonní jako funkce, takže pro každý z nich jde křivka jedním určitým směrem. Abychom zjistili, co se děje, použijeme tabulku a selský rozum (připomeňme, že kladné znamená, že křivka jde doprava, a záporná znamená, že jde doleva, podobně určuje směr nahoru či dolů).

Než načrtneme, co jsme zrovna zjistili, určíme body obratu v rovině dosazením kritických hodnot parametru do x a y. Napíšeme si také výsledné body s přesností na jedno desetinné místo, abychom je mohli nakreslit.

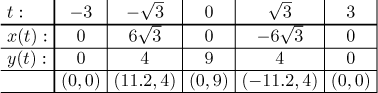
Teď můžeme nakreslit obrázek.

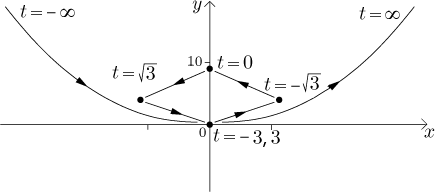
Jak už jsme diskutovali v části Teorie, každý úsek, který jsme zrovna identifikovali, lze považovat za graf nějaké funkce y = y(x). Pro derivaci této funkce máme vzorec.

Teď určíme monotonii těchto funkcí (připomeňme, že každý úsek může být popsán jinou funkcí).

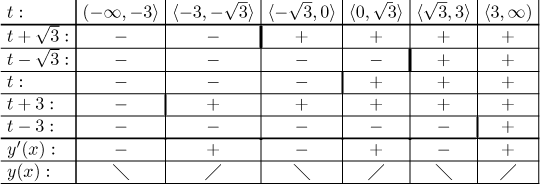
Jak toto interpretujeme? Například hodnotám parametru t mezi 0 a odmocninou ze 3 odpovídá úsek, který jde z (0,9) dolů a doleva. Jako graf funkce je nicméně rostoucí.

Tento způsob pohledu je užitečný, protože nám umožňuje graf zpřesnit tím, že uvažujeme konvexitu. Použijeme vzorec pro druhou prostorovou derivaci y(x).

Jediné kritické body jsou plus a mínus odmocnina ze 3. Máme následující konvexitu.

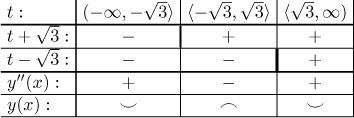
To se shoduje s obrázkem, který nám zatím vycházel. Než uděláme konečný náčrt, spočítáme si body pro několik dalších hodnot parametru dosazením do x a y, zaokrouhlíme je na jedno desetinné místo.

Teď namalujeme náčrt křivky.

Zpět na Řešené příklady - Implicitní a parametrické funkce