Nejprve zavedeme pojem spojitosti po částech:

Definice
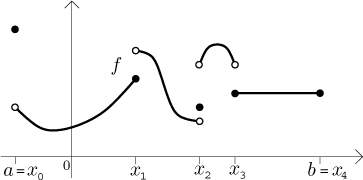
Řekneme, že funkce f je po částech spojitá na intervalu ⟨a,b⟩, jestliže existuje konečná množina bodů a = x₀ < x₁ < . . . < x_N = b takových, že pro každý úsek ⟨x_k−1,x_k⟩, kde k = 1,...,N, má funkce f limitu v x_k−1 zprava, limitu v x_k zleva a je spojitá na (x_k−1,x_k).

Zde je typický příklad po částech spojité funkce:

Máme následující tvrzení:

Věta
Jestliže je funkce po částech spojitá na uzavřeném intervalu, pak je tam Riemannovsky integrovatelná.

Po částech spojité funkce jsou velmi užitečné, protože se často používají v aplikacích.

Ve skutečnosti ani nekonečně mnoho - ale spočetně - bodů nespojitosti nepředstavuje problém. Přesná formulace, kolik bodů nespojitosti je povoleno, vypadá takto:

Věta
Funkce definovaná na uzavřeném intervalu je tam Riemannovsky integrovatelná tehdy a jen tehdy, jestliže množina jejích bodů nespojitosti má nulovou míru.

Ta "míra" ve větě je Lebesgueova míra - což jasně ukazuje, že tohle je hodně přes rozsah tohoto Math Tutoru.