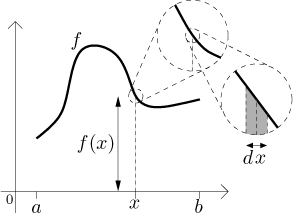
The idea of the Riemann integral is based on the approximation by rectangles. If f is Riemann integrable, then the error of approximation for really narrow rectangles is almost zero. What is the narrowest possible rectangle? This question has no answer, since the thickness can be made arbitrarily small, the limit case being a rectangle of zero thickness, which is no rectangle at all.
Now we introduce the differential dx, which is a little piece of the x-axis that is infinitely small (but its length is not zero). Of course no such thing is really possible, but the beauty of this concept is that if one is careful in using it, it seems to work; what is more important, thinking in terms of dx can make many mathematical notions seem more natural and easier. This is the reason why most mathematicians, although well aware that there are no infinitely small pieces of the x-axis, still use the concept of dx when thinking about problems. Of course, any conclusions that they reach this way then have to be properly checked and justified. We will now apply the dx approach to the notion of the definite integral.
Since dx is infinitely small, any real rectangle will be thicker than an imaginary rectangle which is dx wide. So a rectangle of thickness dx is the narrowest possible rectangle, in other words, the error of approximation will be negligible. This is in part given by the fact that any piece of the graph of f that is dx wide will be so small that we can assume (without making an error) that it is a straight line. We try to show it in this picture, where we enlarge a little piece of graph:

Thus the region under this piece is exactly a trapezoid (horizontal base on
the x-axis, vertical sides, and a straight line on the top). Its area
can be calculated by multiplying its base dx by the height measured in
the middle of it, which is
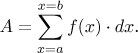
Of course, this sum makes no sense (but this should not be surprising, we started by introducing a non-existent infinitely small piece of the x axis). Why is it so? If we split the region under the graph into strips whose thickness is infinitely small, how many are of these? The answer is obvious: infinitely many. Not just that, there is uncountably many such trapezoids and therefore we do not really know how to add their areas, we only know how to add up finitely many or countably many numbers. The fact that this summing up business is somehow fishy is expressed by replacing the summation sign with the integral sign:
![]()
We emphasize again that the above reasoning was not rigorous, however, this thought process seems intuitive and very often works well. If you get used to the idea of dx as an infinitely small piece of the x-axis, many other formulas become easy to see (volume, center of gravity etc).
For more information about dx see Leibniz notation in Derivatives - Theory - Introduction.