Recall that this function looks to our imperfect eyes like two lines,

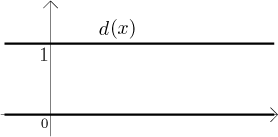
but in fact those lines consist of infinitely many dots with infinitely many gaps between them. For details see Functions - Theory - Elementary functions - Dirichlet function.

We claim that this strange function is not integrable on any closed interval. Consider numbers a < b. We will prove that f is not Riemann integrable on [a,b].

Indeed, pick any partition P of [a,b]. Now consider one of the segments [x_k−1,x_k], where k = 1,...,N.
Since rational numbers are dense, there must be a rational number inside [x_k−1,x_k], and therefore M_k = 1.
Similarly, since irrational numbers are dense, there must be an irrational number inside [x_k−1,x_k] and therefore m_k = 0.

Consequently,

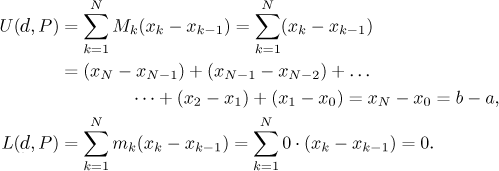
This is true for any partition P, therefore

and the function is not Riemann integrable on [a,b].