First we define the notion of piecewise continuity:

Definition
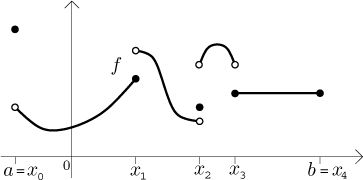
We say that a function f is piecewise continuous on an interval [a,b] if there is a finite set of points a = x₀ < x₁ < . . . < x_N = b such that for every segment [x_k−1,x_k], where k = 1,...,N, the function f has a limit at x_k−1 from the right, limit at x_k from the left, and is continuous on (x_k−1,x_k).

Here is a typical example of a piecewise continuous function:

We have the following statement:

Theorem
If a function is piecewise continuous on a closed interval, then it is Riemann integrable there.

Piecewise continuous functions are useful because they are often used in applications.

Actually, even infinitely many - but countably many - points of discontinuity do not pose a problem. The precise statement concerning how many points of discontinuity are allowed is this:

Theorem
A function defined on a closed interval is Riemann integrable there if and only if the set of its points of discontinuity is of measure zero.

The "measure" in this statement is the Lebesgue measure - which clearly shows that this is way beyond the scope of this Math Tutor.