Typické integrály:

Příklad	Šuplík
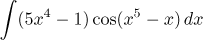	Substituce Zde y = x5 − x.
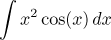	Integrace per partes
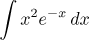	Integrace per partes
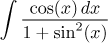	Substituce Zde y = sin(x). Pasuje také do šuplíku "goniometrické integrály", ale tam se doporučí přesně tato substituce.
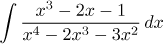	Racionální lomená funkce (rozklad na parciální zlomky)
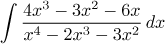	Racionální lomená funkce (rozklad na parciální zlomky) Lépe: substituce (čitatel je derivace jmenovatele)
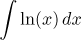	Integrace per partes
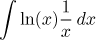	Substituce Zde y = ln(x).
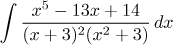	Racionální lomená funkce (rozklad na parciální zlomky)
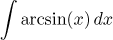	Integrace per partes
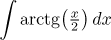	Integrace per partes
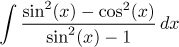	Geoniometrický integrál. Buď univerzální substituce y = tg(x/2), nebo v tomto případě také lehčí y = tg(x).
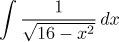	Integrál s odmocninou z kvadrátu Obecná metoda: Nepřímá substituce x = 4sin(t). Zde je snadnŘjší varianta, vytknutí vede na tabulkově integrál.
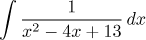	Racionální lomená funkce DoplnŘní čtverce a vytknutí vede na tabulkový integrál

Dobře připravený student by měl být schopen určit tyto odpovídající šuplíky již při pohledu na integrál. Ačkoliv tento seznam rozhodně nepokrývá všechny typy integrálů, zkušenost naznačuje, že pokud je student opravdu dobře obeznámen s těmito typy, měl by zvládnout většinu integrálů.