Příklad:

Nabízí se substituce

Příslušný výraz pro dy v integrálu není, tak si upravíme vzorec pro transformaci difereniciálu do příhodnější polohy.

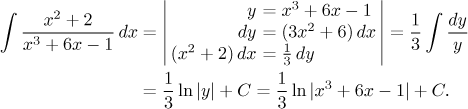
Integrál platí na intervalech, kde jmenovatel zlomku není nulový.

Mohli jsme si také pomoci algebraickou úpravou integrálu: vynásobit čitatel trojkou, aby se shodoval s výrazem pro dy, pak vydělit integrál třemi. Tento algebraický trik si ukážeme na dalším příkladě.

Příklad: Podívejme se na následující integrál. Zde je díky složené funkci jasným kandidátem substituce y = 1 − x². Abychom uspěli, budeme v integrálu potřebovat −2xdx, tak si to ještě před zahájením substituce připravíme. Budeme pak ale také muset odvodit ze základní substituční rovnosti vzorec, který nám umožní převést čitatel.

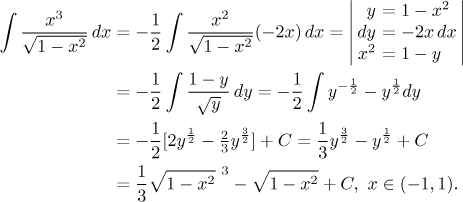
Příklad: Uvažujme integrál

Zde nám vadí ta odmocnina. Zkusíme se jí zbavit substitucí, ale její úspěch není zřejmý, protože evidentně nepasuje nejlépe.

Musíme se tedy pokusit vytvořit vzorec pro dx, přičemž je třeba jej udělat tak, aby na druhé straně byly je y, neboť v novém integrálu nemohou být žádné x. Budeme také potřebovat vzorec pro x, ale to je snadné.

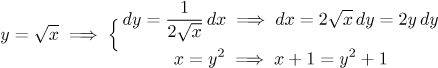
Protože jsme dokázali vyjádřit všechny výrazy v integrálu pomocí proměnné y, můžeme provést substituci:

Toto je integrál z racionální lomené funkce, který hravě spočítáme pomocí parciálních zlomků, viz tento příklad v části Řešené příklady - Integrace.

Poznámka: Někdy se dá výpočet výrazně zjednodušit, pokud začneme s algebraickými úpravami hned od počátku. V tom příkladě výše jsme nejprve odvodili transformační vzorec pro diferenciály a pak z něj vytáhli dx. Je to mnohem snažší, pokud pořadí obrátíme: Nejprve z původní rovnice spočítáme x (čímž z toho vlastně vznikne nepřímá substituce) a odtud již přímo derivací dostaneme dx.

Příklad: Uvažujme integrál

Zde by se výraz zjednodušil, pokud by místo exponenciál bylo písmeno, nabízí se tedy substituce y = e^x. V integrálu by se silně hodilo mít e^xdx, ale není to tam, tudíž si musíme vyrobit pro to vzorec. Zkusíme to oběma způsoby, nejprve přes vzorec pro diferenciály, pak přes nepřímou substituci.

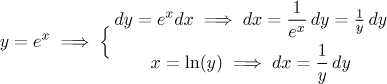
Vyšlo to, proto

Tento integrál se snadno spočítá pomocí parciálních zlomků. Je užitečné si zapamatovat, že při exponenciální substituci nikdy není problém dx.

Příklad: Uvažujme následující příklad.

Zde bychom se rádi zbavili goniometrických funkcí, ale nejprve musíme rozhodnout, zda budeme substituovat za sinus nebo kosinus. Víme, že když použijeme y = sin(x), tak budeme potřebovat cos(x)dx, zatímco substituce y = cos(x) vyžaduje -sin(x)dx. Máme šanci tam něco takového vyrobit? Evidentně jediným možným zdrojem je čitatel, ze kterého bychom sinus vytahovali těžce, ale kosinus by vytáhnout šel. To ukazuje na sinovou substituci, budeme pak také ale potřebovat vzorec pro kosinus ve jmenovateli.

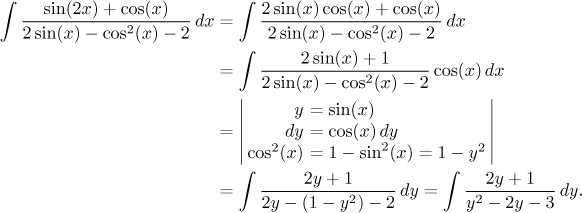
Substituce prošla a nový integrál se hravě udolá přes parciální zlomky.