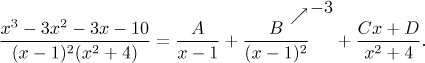
Zde ukážeme několik metod, které lze použít k určení neznámých konstant v rozkladu na parciální zlomky. Budeme je ilustrovat na rozkladu

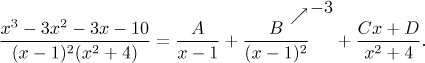
Jednu konstantu jsme již určili zakrývací metodou, protože ta je nejjednodušší a nemá smysl hledat k ní alternativu. Ostatní konstanty bychom standardně určili násobící metodou, což je přesně chvíle, kdybychom ocenili nějakou alternativu.

Lineární faktory 1.
Začneme s problémem nalezení A, obecně s hledáním konstant u lineárních faktorů, které se objevují ve vyšší mocnině. První zajímavá metoda je založena na selském rozumu. Pomocí zakrývací metody určíme A_n odpovídající nejvyšší přítomné mocnině jistého lineárního faktoru (x − a)ⁿ. Jakmile tento koeficient známe, tak lze přesunout celý parciální zlomek nalevo a spojit s původním podílem, teď se A_n−1 stává koeficientem s nejvyšší mocninou napravo a můžeme k jeho nalezení použít zakrývací metodu (s novou levou stranou). Jakmile tak učiníme, přesuneme zase tento zlomek doleva a pokračujeme tímto způsobem, dokud nedostaneme všechny koeficienty odpovídající tomuto lineárnímu faktoru. Pak se přesuneme k dalšímu atd., takže sa takto nakonec dají určit všechny konstanty u parciálních zlomků založených na lineáře. Jak to zabere u našeho příkladu?

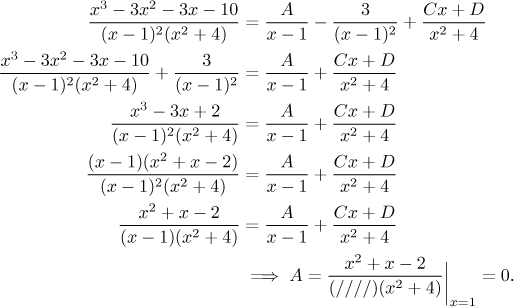
Takže jsme A našli, ale úprava podílu nalevo dala asi víc práce než celá násobící metoda. Mohou ale být příklady, kte toto pomůže.

Lineární faktory 2.
Zde se pokusíme zobecnít zakrávací metodu. Připomeňme, že je založena na následujícím postupu. Vezmeme rozklad, který se soustředí na nějaký lineární faktor (x − a)ⁿ, a vynásobíme jej tímto faktorem.

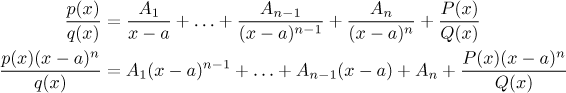
Pak jsme dosadili x = a a dostali A_n. Dá se nějak dostat i A_n−1? Ano, můžeme zderivovat obě strany této rovnosti, čímž A_n zmizí A_n−1 tak bude jako konstanta, takže dosazení už to udělá. Zase to použijeme na náš příklad.

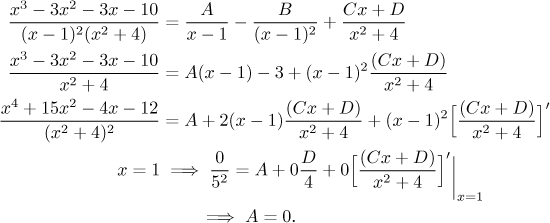
Osobně bych raději dělal násobící metodu. Pokud derivujeme vícekrát, dostaneme také další konstanty. To je zajímavé z teoretického hlediska, protože dostáváme obecný vzorec pro všechny konstanty u zlomků s lineárami. (Pokročilí čtenáři mohou vidět zajímavou souvislost s rezidui a obecně Laurentovým rozvojem komplexních funkcí.)

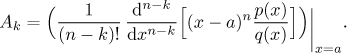
Kvadratické faktory 1.
Zde je možné použít zajímavou verzi dosazovacího triku. Konstanty u lineárních faktorů (u nejvyšších mocnin) lze získat dosazovaním kořenů lineár, u konstant z kvadratických parciálních zlomků nejvyšších mocnin zase zabere dosazení komplexního kořene.

U našeho příkladu má komplexní faktor kořen x = 2i, jeho dosazením dostaneme

Porovnáním reálné a imaginární části získáme rovnice 2 = 8C − 3D a 14 = 6C + 4D, které hravě vyřešíme a dostaneme C = 1 a D = 2.

V případě, že by jeden kvadratický člen byl přítomen vícekrát, získáme zase pouze koeficienty u nejvyšší mocniny.

Kvadratické faktory 2.
Pokud vám nevadí komplexní výpočty, nabízí se ještě jeden trik. Pokud povolíme komplexní kořeny, tak lze každou ryzí racionální funkci rozložit na parciální zlomky založené na lineárních členech neboli na těch nejpříjemnějších. Vzniknou pak i komplexní koeficienty. V našem příkladě dostaneme

Teď můžeme použít zakrývací trik s příslušnými kořeny a dostaneme b, c a d, u posledních dvou to bude

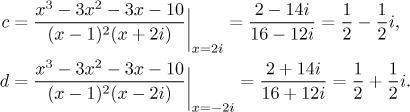
Poslední konstantu A = 0 získáme například jednou z metod výše, takže

Získali jsme tak rozklad, jehož další výhodou je, že nemá kvadratické členy, takže jej vlastně integrujeme zpaměti:

Nevýhody jsou dvě. Museli jsme provádět dost hnusné komplexní výpočty, což možná některým nebude až tak vadit. Větším problémem je, že výsledek integrace obsahuje komplexní čísla, jenže zadaná funkce je reálná. Výsledek by tedy měl být rovněž reálný, takže se získaný komplexní výsledek integrace ještě musí upravovat do reálného tvaru, což nemusí být jednoduché (a většinou rozhodně není). Snad z toho důvodu se tento trik s komplexním rozkladem nepoužívá pro integraci v reálném oboru.