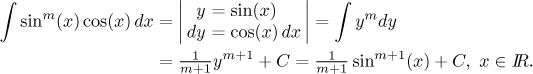
Nejprve si odvodíme vztah pro sinus. Začneme jedním přípravným integrálem, který pak použijeme při vlastním výpočtu:

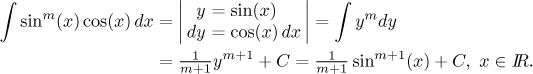
Ve výpočtu integrálu z mocniny sinu nejprve uděláme goniometrický trik, načež použijeme metodu per partes:

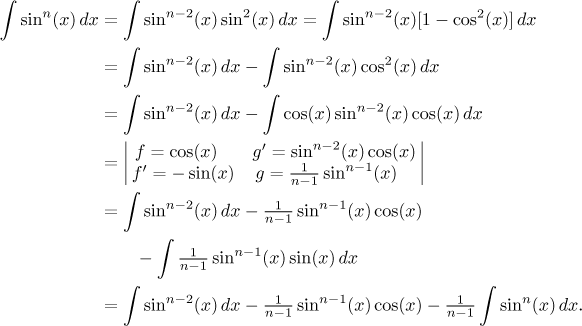
Dostáváme rovnici, ve které převedeme integrál z n-té mocniny z pravé strany na levou:

Když převedem zlomek z levé strany na pravou, získáme kýžený vztah pro integrál z mocniny ze sinu. Podobným způsobem integrujeme n-tou mocninu z kosinu.

Nyní se podíváme na mocninu tangensu. Ta se po algebraickém triku dá již přímo spočítat substitucí:

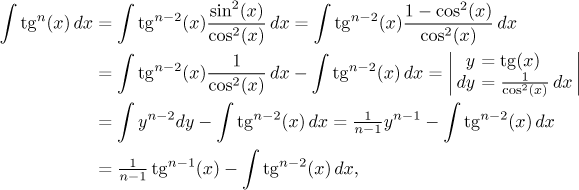
přesně jak jsme slibovali. Integrál z mocniny kotangensu se zase dělá obdobně.

Nakonec si odvodíme integrál z mocniny sekansu (kosekans se integruje obdobně). Dělá se algebraickým trikem a metodou per partes, nemusíme ale řešit rovnice. Pro per partes si nejprve spočítáme jeden integrál:

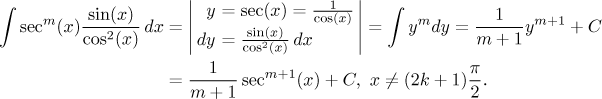
A teď už můžeme počítat:

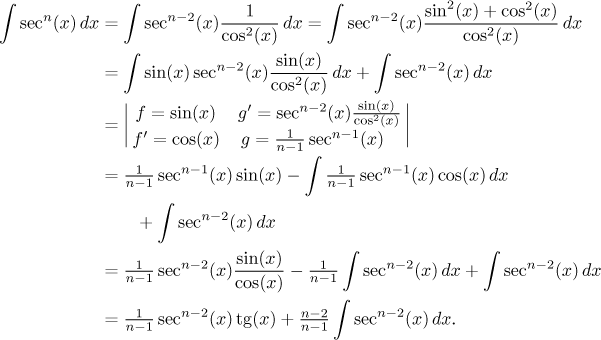
Zkuste si sami odvodit redukční formule pro kosinus, kotangens a kosekans, je to dobré cvičení.