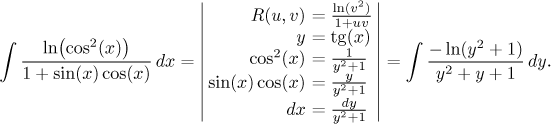Uvažujeme integrál typu
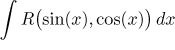 ,
kde R(u,v) je libovolná funkce dvou
proměnných definovaná na jednotkové kružnici; budeme předpokládat, že se v
této funkci jako takové již nevyskytují goniometrické funkce. Pak je možno
použít univerzální substituci a obdržet integrál, ve kterém se již
nevyskytují goniometrické funkce. Víme už ale, že to je metoda nejvyšší
nouze, tak se teď podíváme na podmínky, které nám umožní použít jednodušších
substitucí.
,
kde R(u,v) je libovolná funkce dvou
proměnných definovaná na jednotkové kružnici; budeme předpokládat, že se v
této funkci jako takové již nevyskytují goniometrické funkce. Pak je možno
použít univerzální substituci a obdržet integrál, ve kterém se již
nevyskytují goniometrické funkce. Víme už ale, že to je metoda nejvyšší
nouze, tak se teď podíváme na podmínky, které nám umožní použít jednodušších
substitucí.
1. Pokud pro všechna u, v na jednotkové kružnici
platí
R(−u,v) = −R(u,v),
pak můžeme použít substituci
y = cos(x).
Vlastně to tedy znamená, že uvažujeme integrály typu
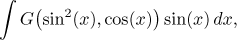
kde funkce G jako taková neobsahuje goniometrické funkce.
Příklad:
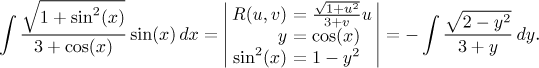
2. Pokud pro všechna u, v na jednotkové kružnici
platí
R(u,−v) = −R(u,v),
pak můžeme použít substituci
y = sin(x).
Vlastně to tedy znamená, že uvažujeme integrály typu
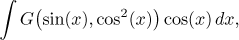
kde funkce G jako taková neobsahuje goniometrické funkce.
Příklad:
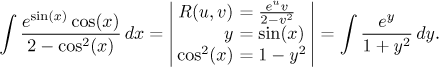
3. Pokud pro všechna u, v na jednotkové kružnici
platí
R(−u,−v) = R(u,v),
pak můžeme použít substituci
y = tg(x).
Vlastně to tedy znamená, že uvažujeme integrály typu
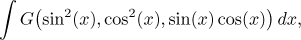
kde funkce G jako taková neobsahuje goniometrické funkce.
Příklad:
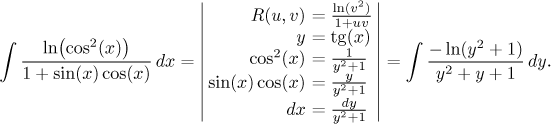
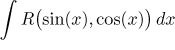 ,
kde
,
kde 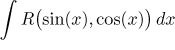 ,
kde
,
kde ![]()
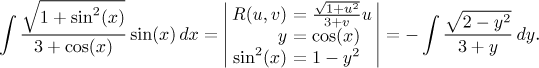
![]()
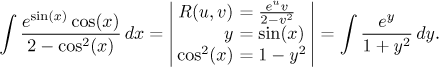
![]()