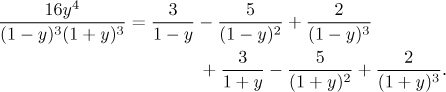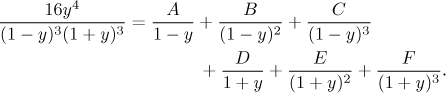
Potřebujeme dokončit rozklad
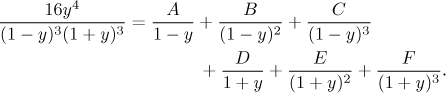
Dva koeficienty snadno získáme zakrývací metodou.
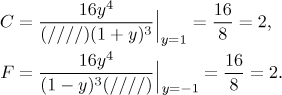
Teď potřebuje získat čtyři rovnice k určení zbývajících konstant. Standardní postup je použít násobící metodu, která je založena na obecném rozkladu, kde vynásobíme jmenovatelem. Použijeme znalost dvou z konstant.
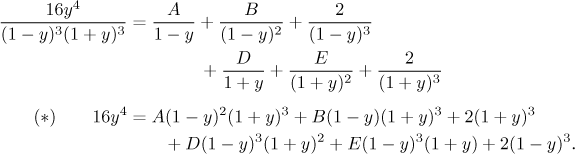
Teď bychom měli roznásobit členy napravo a přepsat si pravou stranu jako polynom. Porovnáním koeficientů se pak dostanou rovnice. Klidně si to zkuste, zde se podíváme po snadnějších alternativách. Jednu rovnici určitě dostaneme limitním trikem, kde původní rovnici vynásobíme výrazem y a pak přejdeme do nekonečna.
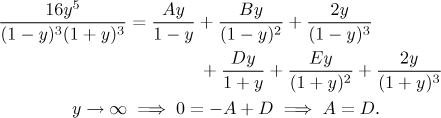
Jednu máme, tři zbývají, zkusíme dosazovací trik a dosadíme do (*) nějaké pěkné hodnoty za y. Víme, že nemá smysl dosazovat kořeny, protože to je ekvivalentní zakrývacímu triku. Zkusíme tedy jiná pěkná čísla, pak vyřešíme vzniklé rovnice.
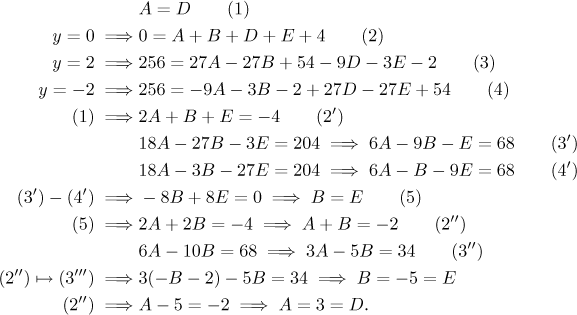
Protože rovnice měly jistou symetrii, použili jsme eliminaci, můžete samozřejmě ony čtyři rovnice vyřešit svou nejoblíbenější metodou. Je hotovo.