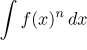Box "trigonometric integrals"

We start by looking at trigonometric integrals. If you came here for hyperbolic functions, see the note at the end.

Integrals from expressions involving trigonometric functions appear quite often. For many of them there are standard procedures, many can be also found in lists of integrals. In most cases it is enough to know how to integrate various combinations of sines and cosines, as all other trig functions can be written using these two. However, this sometimes leads to complicated expressions, so we will also look at some popular combinations of tangents and cotangents. And finally, since secant and cosecant are sometimes used, we will pay some attention to these, too. As a last resort we cover the universal substitution. Because general methods usually lead to long calculations, we will start with types of integrals for which there are more convenient procedures.

 •  Type 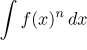, where f is some trigonometric function and n is a positive integer. For this type of integrals we have reduction formulas that hold for integers n greater than or equal to 2:

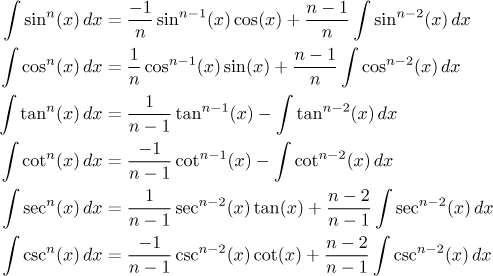
These formulas can be deduced using trig identities and integration by parts, as you can see here. This is a good opportunity for a note concerning the usefulness of secants and cosecants: Notice that the reduction formulas only work for positive n! This means that if you have a cosine or sine in the denominator in a positive power, then you have to use the secant, respectively cosecant formulas.

Since every application of a reduction formula decreases the power by two, there are two possibilities:

1. If n is even, the corresponding trig function eventually disappears and we end up integrating a constant. Example:

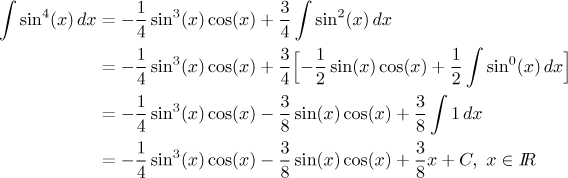
2. If n is odd, we end up integrating some trigonometric function. Sine and cosine are elementary integrals and thus we should have no trouble. Example:

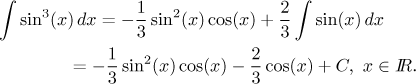
Now we look at the remaining four trig functions, we start with tangent:

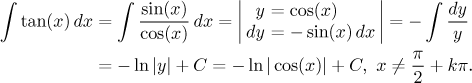
This result can be also written as follows:

Cotangent is integrated in a similar way, as we already saw in Theory - Methods of integration - Substitution.

Secant and cosecant rarely appear as such, more often we encounter them in the form of reciprocal cosine and sine. These integrals are a bit tougher: We have to use the add-subtract trick (or, more precisely, multiply-divide), substitution and partial fractions:

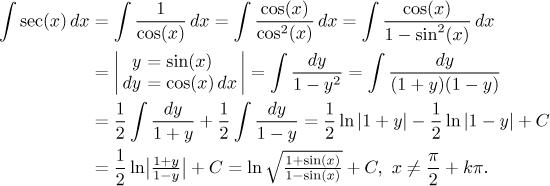
An alternative solution suitable for those really familiar with secants and cosecants is here.

Since the integral of cosecant is done similarly, we just quote the answer:

Note: When integrating reciprocal sine or cosine, it is good to remember that the second power in the denominator is actually an elementary integral:

Important remark: If we integrate an odd power of sine or cosine, we can avoid the repetitive use of reduction formulas. Instead, we can separate one sine or cosine which we use for substitution, and the remaining sines (or cosines) can be easily changed to the complementary function (the power is even now). An example explains it best:

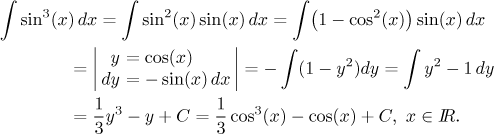
Note that if n is even, then this substitution trick does not help. It is the presence of an "extra sine" or "extra cosine" that makes substitution possible - and it is also a clear indication that we should use it. After all, we already saw this happening when we integrated tangent and secant. Note that in secant, the "extra cosine" is in the denominator; however, we did not mind, because we were able to move it into the numerator easily.

Another alternative - sometimes very effective - is to reduce the power using various trigonometric identities. This brings us to the next type where we look closer at this method.

 • Type 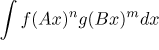, where f and g are sines and/or cosines.

These integrals are best solved using trig identities. It is usually easier if you first reduce powers using

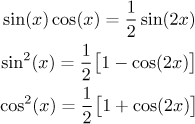
Typically one would start using the first formula to eliminate all possible products sin(Ax)cos(Ax) and then use the other two on all powers that are left. Roughly speaking, these identities allow us to halve powers in exchange for doubling arguments.

In the end we are left with products of the form f (Ax)g(Bx) with A ≠ B, where the above identities do not help. But we have another set of identities handling exactly this case:

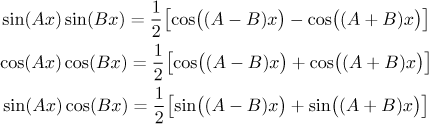
Example:

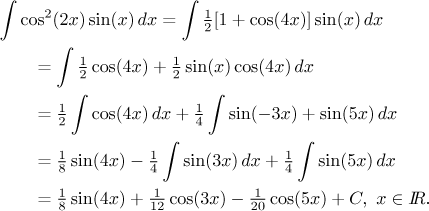
However, there is an opposite strategy, where we try to use identities to remove multiples at the variable, usually in exchange for powers, in general we thus arrive at a linear combination of integrals with expressions sin^m(x)cosⁿ(x), which sounds tempting. Disadvantage of this procedure is that one never knows beforehand whether it ends up well or not. While the previous procedure always leads to integrals that can be easily integrated using linear substitutions, here it is a lottery, because one has to use approaches from the next type below.

If one of the numbers m, n is even and the other odd, then integrating such an expression can be relatively simple via a substitution, see the first possibility below. The other possibilities (two odd, two even) are the other extreme, they are so complicated that the first recommended procedure tends to be better. If we try this alternative procedure on our last example above, it turns out that we are very lucky and integrate easily using "extra cosine".

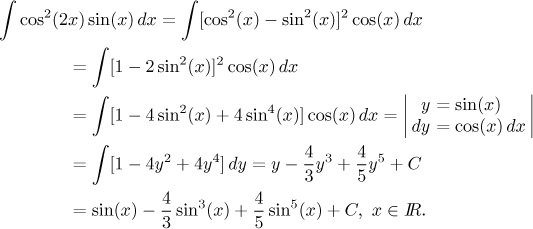
The moral of the story is that we cover some standard procedures here, but a good knowledge of trig identities often offers better possibilities and trig integrals tend to be one-of-a-kind.

For another example we return to the fourth power of sine, which we solved using reduction formulas above and here you can see how it can be done using identities. However, the method of using trig identities can be sometimes quite taxing, for instance this problem is cruel.

 • Type 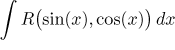, where R is a rational function of two variables. This type of integral is transformed via a suitable substitution to an integral of a rational function, then a standard approach is to apply the partial fractions decomposition and we know how this goes on. This cathegory does not allow directly for multiples of arguments in sine/cosine. However, trig identities can be used to manipulate expressions sin(Ax) and cos(Ax) with A an integer to get rid of this A, so perhaps all reasonable trig integrals (including those above) fit this type and it is worth knowing how to deal with them.

There is a standard universal substitution for this type of trig integrals, but the calculations are usually rather complicated, so we first look at two cases for which we have easier substitutions:

1. The easiest case is when there is an "extra sine" or "extra cosine" in the numerator (or denominator!) and at all other places, sines and cosines have even powers. Then we apply the strategy that we already saw for instance when integrating secant and tangent, here is one more example:

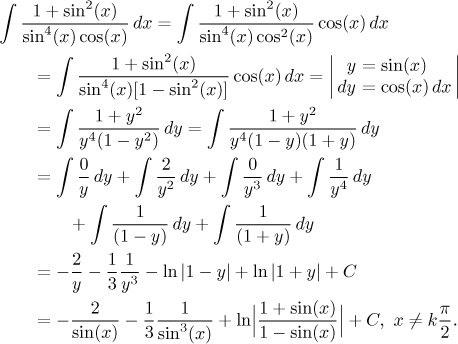
Occasionally we can get away with a similar trick using a tangent substitution - if we can change the integrated function into an expression consisting only of tangents and with extra squared cosine in the denominator. Then the substitution y = tan(x) works. Similarly, we can use the cotangent substitution if we can get the function into a form with cotangents and extra squared sine in the denominator.

2. If all sines and cosines in the integral have even powers, we cannot "borrow" one of them for substitution. Then we use the substitution y = tan(x). Other trig functions can be deduced from this equation. We outline how it is done for sine, cosine is similar:

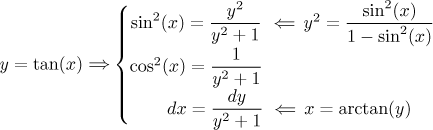
Now we see why this substitution would not work if odd powers appeared. We will show this substitution on a suitable example:

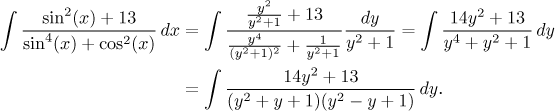
The problem can be finished using partial fractions, a brief sketch is here.

This is not just a formal problem mathematicians love to worry about, there are even simple integrals where this comes up, and in general the procedure for handling it is not exactly simple, we show one such situation in this example in Solved Problems - Integrals. However, we often get lucky and the answer comes up reasonable, so a good strategy is simply to check on what set are the given function and the answer continuous, the integral should work there.

3. If we have a combination of sines and cosines that does not fit the first two situations, then we have to use the dreaded universal trig substitution. Since it is universal, it could have been used to solve all problems that we saw in the trig integrals section; but as we will now see, it is a substitution that one tries to avoid, just look at the transformation equations:

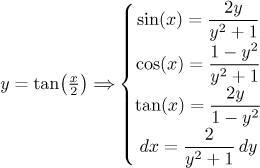
Here you find how to deduce these equations. As you can see, all trig functions can be expressed using powers of y. Example:

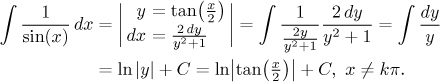
This was actually quite simple (although trying to show that this answer is equal to the one we had above is rather tough). Unfortunately, usually it is a different story. For instance, we will now try to apply the universal substitution to the problem above that we originally solved using the substitution y = tan(x):

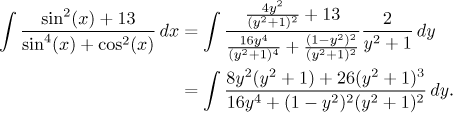
Theoretically we could finish this problem using partial fractions. But note that the denominator is a polynomial of the eighth degree, so it is highly unlikely that we could factor it. As you can see, the universal substitution often leads to rational functions involving polynomials of high degrees, which leads to practical problems. This is a good motivation for always looking for some way to avoid this substitution.

We will now try to apply all these methods to the integral of tan²(x). As a power it can be done by the appropriate reduction formula:

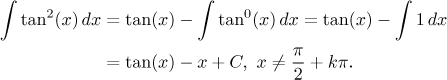
If we write the tangent using sine and cosine and square, we get a reasonable function featuring only even powers of sine and cosine. This means that there is no extra function that would allow us to use a nice substitution, but we can still do better than the universal substitution. Namely, we try the tangent substitution:

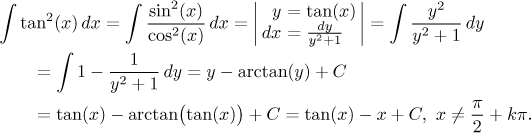
Actually, an experienced integrator would still do something different:

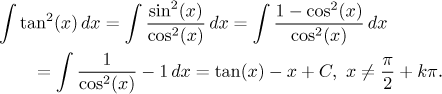
Simply put, knowing identities is the best advice.

Other trig integrals can be found in Solved Problems - Integrals, namely here, here, and here.

Note that in exposition of the last substitutions (sine, tangent and the universal one) we restricted our attention to simpler cases, namely hen R is a rational function. This is not really a problem, since in most cases we use these substitutions in this way, but they also work in more general cases, as we explain in this note. It might come helpful.

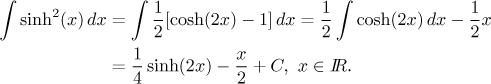
In Solved Problems - Integrals there is a problem whose solution involves a hyperbolic integral. Some examples of hyperbolic integrals are also at the end of the section Methods Survey - Integration - roots of quadratics.

Note that unlike trig functions, hyperbolic functions can be also expressed using exponentials, which opens another possibility for solving hyperbolic integrals. The solution via exponentials is sometimes easier, but often has a serious drawback. The answer would feature exponentials, but since the question is given in the language of hyperbolic functions, we should also express the answer using hyperbolic functions, which may not be easy. But sometimes it is not necessary (for instance with definite integrals), then this trick can be often very efficient.

Next box: integrals with roots of quadratics
Back to Methods Survey - Methods of integration