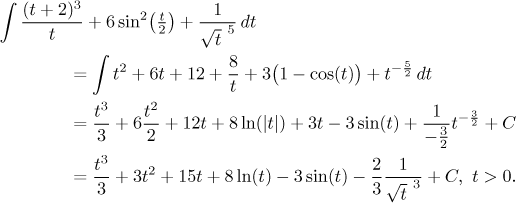Problem: Evaluate the integral
![]()
Solution: This integral is supposed to be solved without any tricks, so obviously we need to rewrite it so that only elementary integrals remain. We take it from the left. In the numerator we can multiply out the power, obtaining simple powers, definitely an improvement. In the second term we have a square of cosine that we do not know how to integrate. Fortunately, there is a trig identity that changes it into an expression that is markedly better, in particular there will be no squaring. Finally, the third term may look intimidating at the first sight, but it is in fact just a power, so we can rewrite it as such.
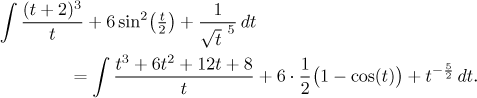
It remains to fix the first term, we easily get rid of the fraction by dividing, we can as well also split the middle term.
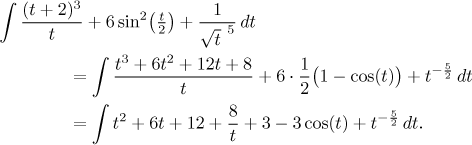
Now we joint the constants and then use linearity to split the integral into many small ones. These we easily integrate separately, they are all elementary integrals. We do not worry about the t there, we know that the name of the variable does not matter and we integrate as usual.
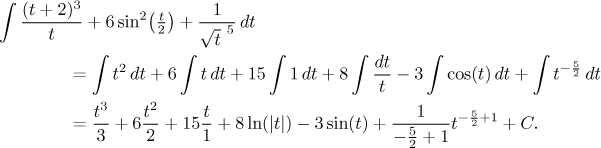
It remains to clean up. Of course we rewrite the terms in a nicer way, we
also need to determine validity of this result. We start with the given
integral, there the term with the square root demands that
We will do one more thing, we rewrite the whole integral again, this time without details that an experienced integrator would do in his head, without writing them down.