Example:
![]()
It seems the following substitution would help:
![]()
We do not have the proper expression for dy in the integral, so we rearrange the differential transformation formula to fit better.
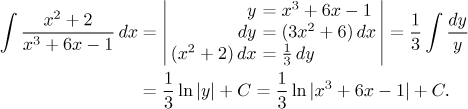
The integral is valid on intervals where the denominator is not zero.
We could have also adjusted the integral algebraically: Multiply the numerator by three so that it coincides with the expression for dy, then divide the integral by three to keep the balance. We will show this approach in the next solution.
Example: Look at the following integral. Here the composed function
clearly points to the substitution
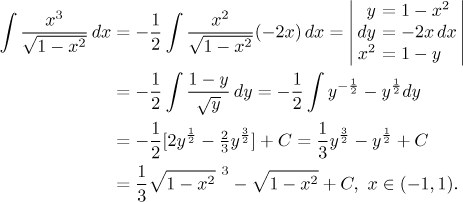
Example: Consider the integral
![]()
Here the square root seems to bother us. We will try to get rid of it by substitution, but its success is not immediately apparent, because it obviously does not fit well.
![]()
We have to try to create a formula for dx, but we have to do it in sucha way that there are only y on the other side, since no x are allowed in the new integral. We will also need a formula for x, but that is simple.
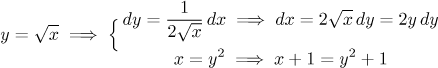
Since we managed to express all parts of the original integral in the language of y, the substitution succeeds:
![]()
We obtained an integral of a rational function, which can be evaluated using the partial fractions approach, see this problem in Solved Problems - Integration.
Remark: Sometimes one can simplify calculations quite a bit by starting with algebraic changes right away. In the above example we first deduced a transformation formula for differentials and then pulled dx out of it. It is much easier if we reverse the order: First solve the basic substitution equality for x (which in fact makes this into an indirect substitution) and then obtain the necessary formula for dx by differentiation.
![]()
Example: Consider the integral
![]()
Here the expression would get markedly better if there was just a letter
instead of those exponentials. This suggests the substitution
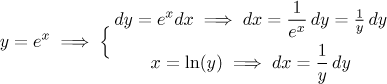
It worked, so
![]()
This is an integral that can be easily evaluated using partial fractions. It is useful to remember that with an exponential substitution we never have problem with dx.
Example: Consider the following problem.
![]()
Here we would like to get rid of trig functions, but first we have to decide
whether we should substitute for sine or for cosine. We know that if we use
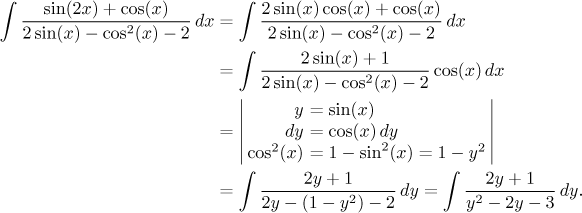
The substitution went through and the new integral is easy to handle using partial fractions decomposition.