Here we will show an alternative way to get from a general partial fraction with a quadratic factor to simpler forms.

The starting point is again the idea that we can use x in the numerator to set up a quadratic substitution, but this time we do not delay it for after getting rid fo the linear part. But if we want to do such a substitution right away, then we need to create the expression 2x + α in the numerator, which is easy using the "add-subtract" method.

We get

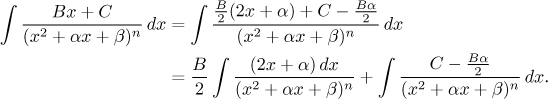
Now we can easily integrate the first integral using the obvious quadratic substitution.

The second integral in decomposition above had only a constant in its numerator, se it is possible to transform it using completion of square into an integral leading to asc tangent, just like in the recommended algorithm.