Here we will show some other methods that can be used to determine unknown constants in a partial fraction decomposition. We will illustrate them on the decomposition

We already determined one constant using the cover-up method, because it is the simplest possible and there is no point in trying to find a replacement for it. The other constants would be normally determined using the multiplying method, which is exactly the moment where we would appreciate some alternatives.

Linear factors 1.
We start with the problem of finding A, in general of finding the other constants related to a linear factor that appears in a higher power. The first interesting method is based on common sense. Using the cover-up method we determine A_n corresponding to the highest present power of a certain linear factor (x − a)ⁿ. Once we know this coefficient, we can move the whole partial fraction to the left and merge it with the original ratio, now A_n−1 becomes the coefficient with highest power on the right and we can use the cover-up method (with a new left hand-side) to find it. Once we do, we again move this fraction to the left and continue in this manner, until we identify all coefficients corresponding to this particular linear factor. Then we move to the next one etc., so in fact all constants in partial fractions based on a linear factor can be identified in this way. How does it work with our example?

So we did find A, but simplifying the ratio on the left was probably more work then the whole multiplying method. Still, there might be problems where this trick is convenient.

Linear factors 2.
Here we will try to generalize the cover-up method. Recall that it was based on the following procedure. We take a decomposition that focuses on some linear factor (x − a)ⁿ and multiply it by this factor.

We then substituted in x = a to obtain A_n. Is there any way to get also A_n−1? Yes, we can differentiate both sides of this equality to make A_n disappear and A_n−1 will be there as a constant, so substituting does the trick now. Again we apply this to our example.

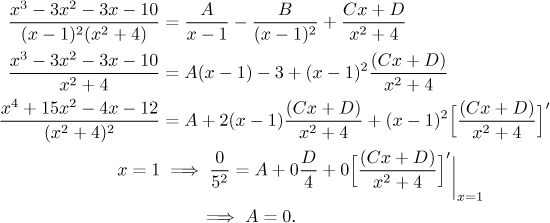
Personally, I'd rather do the multiplying method. If we differentiate more times, we get also to other constants. This is interesting from a theoretical point of view, since we obtain a general formula for all constants at fractions with linear expressions. (Advanced readers may find an interesting connection with residua and in general with Laurent expansion of complex functions.)

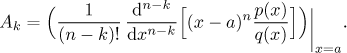
Quadratic factors 1.
Here one can use an interesting version of the plug-in trick. Constants at linear factors (at the highest powers) can be obtained by substituing roots of linear factors, constants at quadratic partial fractions of highest power can be reached by substituting complex roots.

In our example the complex factor has a root x = 2i, plugging it in we get

By comparing the real and imaginary parts we obtain equations 2 = 8C − 3D and 14 = 6C + 4D and solve them easily, getting C = 1 a D = 2.

If some quadratic factor is present in a higher power, this trick will again only help with the partial fraction corresponding to the highest power.

Quadratic factors 2.
If you do not mind working with complex numbers, there is still another trick. If we allow complex roots, then every proper rational function can be decomposed into partial fractions associated with linear factors only, that is, with the most conveinent ones. We then also get complex coefficients. In our example we would get

We can now use the cover-up trick with appropriate roots to find b, c and d, the last two go

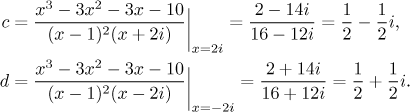
The last constant A = 0 can be obtained for instance using one of the methods above, so

We therefore obtained a decomposition whose advantage is that all the factors ale linear, which means that we can easily integrate it:

There are two disadvantages to this approach. First, the complex calculations were quite difficult, but for some that may not be such a big problem. What really is a problem is that the answer contains complex numbers, whereas the question only deals with real numbers. Thus the answer should be somehow algebraically simplified so that we get rid of all complex numbers, and this can be very difficult (and usually is). Perhaps this is the reason why people tend to avoid this complex decomposition approach when dealing with real integrals.