Here we will take a good look at the substitution situation

The expression under the root cannot be negative, which yields the inequality | y| ≥ A, hence we obtain two intervals for y. Since integration works on intervals, we need to deal with each of this intervals separately and determine on which interval J we will consider the investigated substitution.

Requirements on this interval J are as follows: The function A/cos(t) must be 1-1 on it, that is, the function cos(t) must be 1-1 on it, at the same time this interval should be so large that values of the substitution formula on J should cover the whole necessary interval for y. Also, we will naturally look for such a J within the basic period of cosine. We start with positive values of y.

This choice satisfies all requirements on J. Since on this interval both sine and cosine are non-negative, we also have

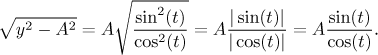
Thus in this case we can ignore the absolute value. Now we look at the version with negative values of y.

This choice satisfies all requirements on J. Since on this interval the sine is positive and cosine negative, we this time have

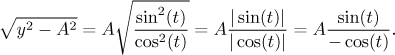
So we see that indeed we are then evluating a different integral.