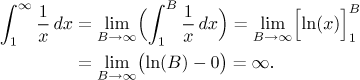
Zde se podíváme na několik příkladů konvergentních a divergentních nevlastních integrálů, abychom viděli, co se může pokazit. Nejprve se podíváme na funkci, která v nekonečnu konverguje k nule, ale ne dostatečně rychle:

Příklad:

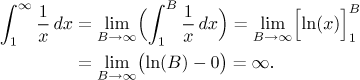
Ačkoliv má mezi 1 a nekonečnem graf funkce 1/x stejný tvar jako graf 1/x², ten podstatný rozdíl je v tom, že druhá funkce se přibližuje k ose x mnohem rychleji. Tento příklad ukazuje, že pokud f konverguje v nekonečnu k nule, tak konvergenci integrálu nepoznáme jen tím, že se podíváme na graf.

Na druhou stranu, pokud je f spojitá, kladná a konverguje v nekonečnu k nenulovému číslu, pak její integrál do nekonečna bude divergovat. V následujícím příkladě to jde vidět už z grafu. Zkusíme si symetrickou situaci s mínus nekonečnem, ať se s ní také seznámíme:

Příklad:

Protože daná funkce konverguje v −∞ do nekonečna, obsah plochy pod ní by také měl být nekonečný:

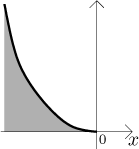
A opravdu,

Teď se podíváme na dva nevlastní integrály s problémem ohledně omezenosti; v typickém případě to znamená, že má funkce svislou asymptotu.

Příklad:

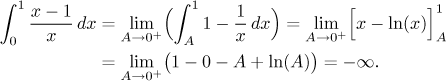
Příklad:

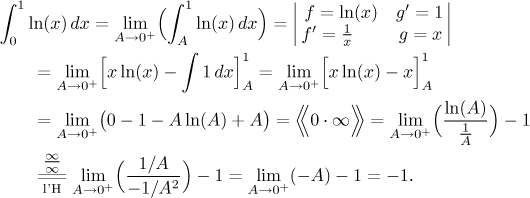
Všimněte si, že ty dvě funkce, které jsme zrovna integrovali, mají grafy v zásadě stejného tvaru mezi 0 a 1:

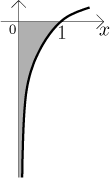
Ten podstatný rozdíl je tu zase v tom, že u druhé funkce se graf přibližuje ke své svislé asymptotě (ose y) mnohem rychleji, než u první funkce, takže nemá čas nashromáždit nekonečný obsah, ačkoliv ta oblast pokračuje bez konce dolů.

Teď se už dostáváme k poslednímu příkladu. V předchozích čtyřech jsme pracovali s funkcemi, které zachovávaly znaménko - byly buď vždy kladné, nebo vždy záporné. Problém konvergence se pak značně zjednodušil: buď jsme měli konečný obsah, nebo ne, v kterémžto případě šla ale pořád obsahu přiřadit hodnota, a to nekonečno nebo mínus nekonečno.

Pokud funkce mění hodně znaménko, je ještě třetí možnost:

Příklad:

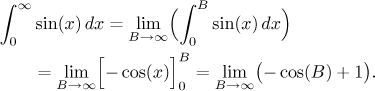
Tato limita neexistuje, tudíž integrál diverguje. V tomto případě ovšem ani nemůžeme dodat nějakou rozumnou odpověď (plus či mínus nekonečno), protože jde o divergenci jiného typu. Vidíme to z grafu:

Když posouváme odřezávací bod B doprava, tak vždy nejprve nahromadíme obsah (jmenovitě 2), pak ale začneme přidávat i oblast pod osou x, což znamená, že přidáváme záporný obsah, jinými slovy ubíráme z předtím získaného obsahu 2. Ze symetrie grafu vidíme, že nakonec ztratíme všechno a na konci periody vždy skončíme s nulou. Když se tedy zeptáme, jestli je nějaká tendence ohledně celkového obsahu, když jdeme s B do nekonečna, odpověď je jednoduchá: ne, žádná tendence není, střídavě nabíráme obsah a pak ztrácíme.

Tato dva druhy konvergence (příliš velká oblast vedoucí k plus či mínus nekonečnu, nebo obsah měnící se neustále, aniž by někam konvergoval, což se stává jen v případě, že funkce mění pořád znaménko) jsou v zásadě jediné dva důvody pro konvergenci. Některé funkce dokonce dokážou oba způsoby zkombinovat, podívejte se například na graf f (x) = x sin(x):

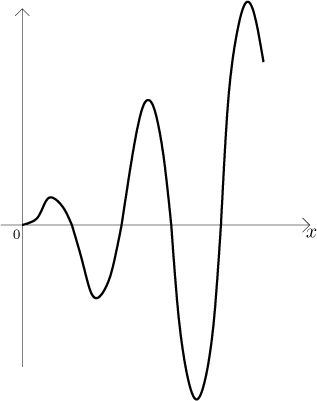
Přesvědčte se sami, že když integrujete tuto funkci od 0 do nekonečna (což necháváme čtenáři, je to jednoduché cvičení na integraci per partes), tak nakonec dostanete limitu, která neexistuje.