Příklad: Rozhodněte, zda tento integrál konverguje:

Řešení: Ověříme, že máme jen jeden problém, jmenovitě nekonečnou horní mez. Máme tedy nevlastní integrál základního typu a můžeme použít testu konvergence. Nejprve musíme najít testovací funkci. To by mělo být snadné, v čitateli a jmenovateli máme polynomy a víme, že když x roste do nekonečna, převáží nejvyšší mocniny.

Nejprve zkusíme, jestli dokážeme získat nějakou nerovnost:

Získali jsme nerovnost, takže zkusíme Srovnávací kritérium. Podíváme se na testovací integrál, což je lehké. Pamatujeme si škálu mocnin a tedy víme, že 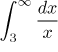diverguje. Bohužel, to je přesně ta situace, kdy Srovnávací kritérium nedokáže dát závěr. Intuitivně bychom viděli, že se nerovnost mezi funkcemi integrací převede na

Tato nerovnost by platila v obou případech, ať už je daný integrál roven číslu nebo nekonečnu, takže odtud nic nevíme. Srovnávací kritérium selhalo.

Teď zkusíme Limitní srovnávací kritérium. Cítíme, že když je x opravdu velké, tak

Tento odhad musí být ověřen:

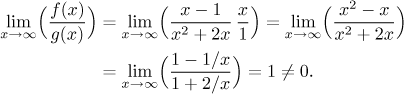
Funkce jsou tedy opravdu v zásadě stejné v blízkosti problematického bodu. Protože testovací integrál 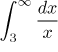diverguje, podle Limitního srovnávacího kritéria diverguje i daný integrál.