Problem: Evaluate (if it converges)
![]()
Solution: If we fail to check on troubles, we would use integration by partial fractions decomposition and obtain
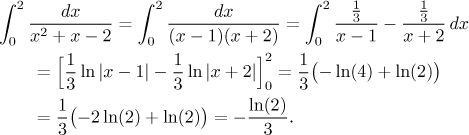
This is, of course, wrong, because as we can see from the decomposition,
there are two points where the denominator is zero. Unfortunately, one of
them, namely
![]()
Since we already determined an antiderivative, we can immediately start evaluating the basic improper integrals; as noted before, it is vital to put the two logarithms together.
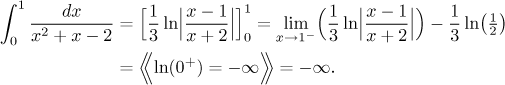
Because the first part ends up divergent, the whole given integral diverges.
Does the given integral exist? To answer that we need to evaluate also its other part.
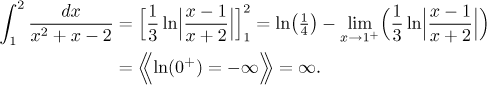
Resulting infinities have opposite signs, so when we add both parts of the
given integral, we get the indeterminate expression