Problem: Decide whether the following integral converges:

Solution: There is just one problem, the infinity, and the given function is positive on the integration interval, so we can apply comparison tests to the given integral. A quick glance shows that evaluation is very difficult if not impossible, so the test approach is a wise decision. We note that if x grows to infinity, then some parts of the expression can be ignored (in both polynomials, only the highest power survives):

Justification:

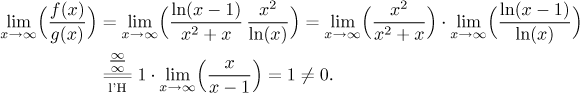
In fact, we even have an inequality there, for x > 2 we have

So with a bit of luck, the Comparison test would work, too. It remains to investigate the test integral. One possibility is a direct computation, first one needs to find an antiderivative using standard integration by parts:

If you don't like working with the logarithm, you can get rid of it by substitution, then apply integration by parts:

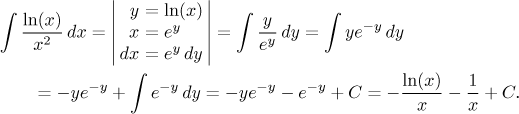
Thus

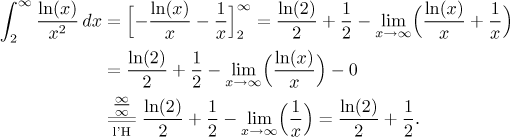
The test integral converges, hence by the Comparison test (or the Limit Comparison test), the given integral also converges.

Note: There is a way to avoid integrating the test function. We observed that logarithm grows slower than any power. Since we have a square in the denominator, we can afford to lose a little bit of it and still obtain a convergent test integral. Precisely, using a limit argument one can show that there is a certain K > 2 such that for all x > K we have . Therefore for x > K we have

We now obtained a different and simpler test function. Since we know that the integral of h from K to infinity converges, by the Comparison Test (and also noting that there are no problems between 2 and K) we conclude that the given integral converges.

Back to Solved Problems - Improper Integrals