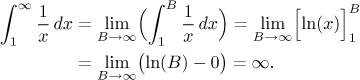
Here we will look at some examples of convergent and divergent improper integrals, so that we can see what can go wrong. First we look at one function which tends to zero at infinity, but not fast enough:
Example:
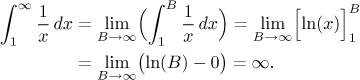
Although between 1 and infinity, the graph of
However, if f is continuous, positive and tends to non-zero number at infinity, the integral to infinity is going to diverge. In the next example this should be already clear from the graph. We try the symmetric situation and use minus infinity to get familiar with it:
Example:
![]()
Since the function tends to infinity at
Indeed,

Now we look at two improper integrals connected with a problem of boundedness; this typically means that the function in question has a vertical asymptote.
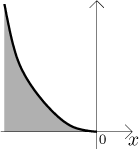
Example:
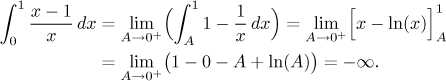
Example:
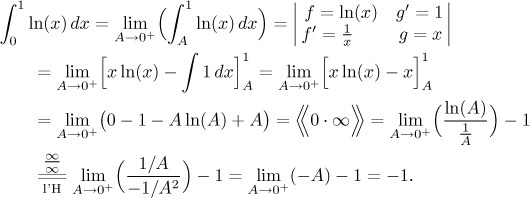
Note that the two functions that we now integrated have graphs of essentially the same shape between 0 and 1:
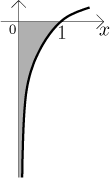
Again, the crucial difference here is that in the latter case, the graph gets really close to its vertical asymptote (the y-axis) much faster than in the former case, therefore it does not have time to accumulate infinite area, although the region keeps going down without ever ending.
Now we get to the last example. In the previous four we dealt with functions that keep their signs. Either they were always negative or always positive. The question of convergence was then quite simple: either there is a finite area, or not, in which case the integral is divergent, but it can still be assigned a value: infinity or negative infinity.
If a function changes its sign a lot, a third possibility appears:
Example:
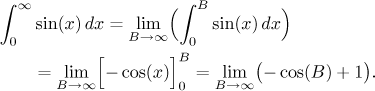
This limits does not exist, therefore the integral is divergent. However, in this case we cannot even assign an answer (plus or minus infinity), because this divergence is of a different kind. We see it from the graph:

As we move the cut-off point B to the right, we always first accumulate some area (namely 2), but then we start including the portion of sine that is below the x-axis, which means that we now include some negative area, in other words, we start losing from the accumulated area 2. By the symmetry of the graph, we eventually lose all and end up with zero area at the end of each period. Thus when we ask, is there some tendency concerning the total area as we go to infinity with B, the answer is: no, there is no tendency.
These two cases of divergence (too much area leading to plus or minus
infinity, or an area that keeps changing without any clear tendency, which
can only happen for functions that keep changing its sign) are essentially
the only two possible causes for divergence. Some functions can even combine
both of these, for instance, look at the graph of
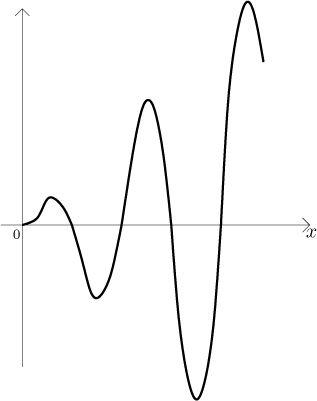
You can convince yourself by integrating this function from 0 to infinity. We leave the actual evaluation to the reader as an exercise (including a standard integration by parts), it should end up with a limit that does not exist.