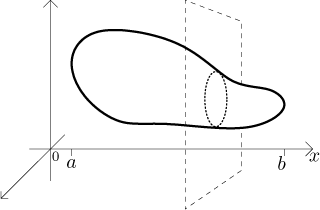
Uvažujme těleso ve třírozměrném prostoru. Pro každé x označíme jako

Objem tělesa je pak roven
![]()
Příklad: Uvažujme jehlan, jehož základnou je pravoúhlý trojúhelník s odvěsnami délky 3 a 4 a jehož výška je 6.
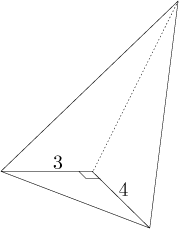
Najděte jeho objem.
Řešení: Protože máme tolik informací o základně, budeme asi řezat jehlan ve směru rovnoběžném se základnou a pokusíme se najít obsahy řezů. Abychom správně postavili problém, umístíme jehlan v prostoru tak, aby byl jeho vrchol v počátku a základna aby byla kolmá na osu x. Poznamenejme, že často se těleso umístí tak, aby počátek ležel v základně, ale v tomto příkladě budeme používat podobnost - umístění, které jsme zvolili, pak povede k jednodušším vzorcům.
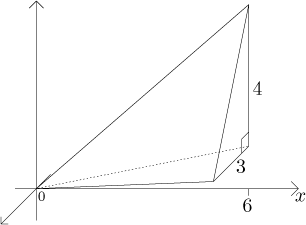
Pokud teď seřízneme jehlan rovinou kolmou na osu x, bude řez paralelní se základnou, rovněž průniky této roviny s jednotlivými stranami jehlanu budou rovnoběžné se stranami základny. Můžeme tedy použít podobnost trojúhelníků.
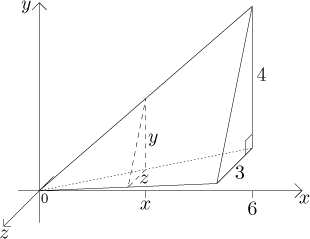
Z obrázku snadno nahlédneme, že
![]()
Pro obsah řezu pak dostaneme (díky pravému úhlu na správném místě)
![]()
Následně
![]()
Všimněte si, že odpověď nezávisela na přesné pozici vrcholu nad základnou, jediná relevantní informace byla jeho výška. Všechny následující jehlany budou tedy mít stejný objem.
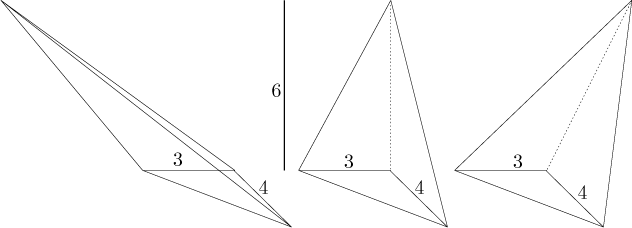
Podobným způsobem lze dokázat následující:
Fakt
Nechť R je rovinná oblast o obsahu A. Pak má jehlan se
základnou R a výškou h objem rovný