Mass and centre of gravity

Segment

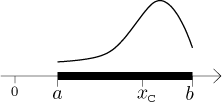
Consider a segment [a,b] on the x-axis with density given by ϱ(x).

Its mass is given by

The centre of mass lies on the x-axis and its x-coordinate is

(Here M_y is the moment of rotation with respect to the y-axis.)

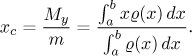
Curve

Consider the graph of a function F on an interval [a,b]. We assume that the density of mass at points of this curve is given by the function ϱ(x).

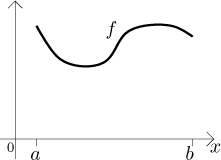
The mass of this curve is given by

Its centre of gravity has coordinates

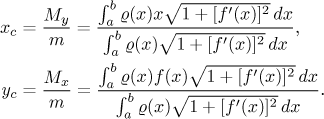
(Here M are the moments of rotation with respect to the respective axes.)

Planar region

Consider a plane region bounded from above by the graph of a function f and from below by the graph of a function g on an interval [a,b]. Assume that the density at points of this region depends only on x and is given by ϱ(x).

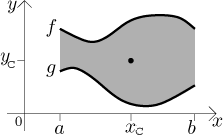
The mass of this region is given by

The centre of mass is given by

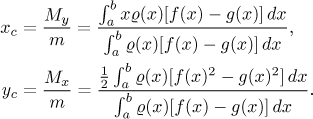
(Here M are the moments of rotation with respect to the respective axes.)

Solid of revolution

Consider the plane region bounded from above by the graph of a function f and from below by the graph of a positive function g on an interval [a,b]. Assume that the density at points of this region depends only on x and is given by ϱ(x).

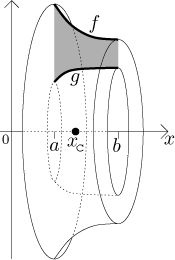
If the region is rotated about the x-axis, the resulting solid has the mass

The centre of mass lies on the x-axis and its x-coordinate is

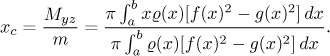
(Here M_yz is the moment of rotation with respect to the yz-plane.)

Note that in all these situations, the most usual setting is when the material is homogeneous, that is, the density is always the same. In such a case the density function ϱ(x) is a constant, hence it cancels from the formulas for center of gravity.

Parametric curve

Consider a parametric curve x = x(t), y = y(t) for t from [α,β]. Assume that y(t) ≥ 0 for all t and that x(t) is increasing:

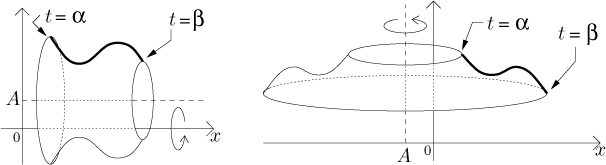
For simplicity we will only consider homogeneous objects. Theor mass can then be calculated as their length/area/volume (see corresponding sections) multiplied by the given constant density. Now we will look at density, in the formulas the density will cancel out.

The center of gravity of the curve itself has coordinates

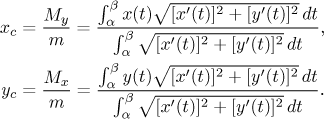
The center of gravity of the region under this curve has coordinates

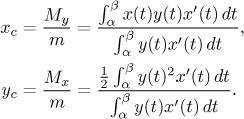
The center of gravity of the surface obtained by revolving this curve about the x-axis lies on this axis and its x-coordinate is

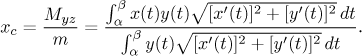
The center of gravity of the solid obtained by revolving the region under this curve about the x-axis lies on this axis and its x-coordinate is

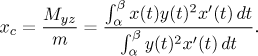
Note that in the last two fractions we cancelled 2π in the second last and π in the last. That is, if you need just the moments, the expressions in these numerators have to be multiplied by these two factors (and in all parametric formulas by the density).

Derivative of an integral
Back to Methods Survey - Applications