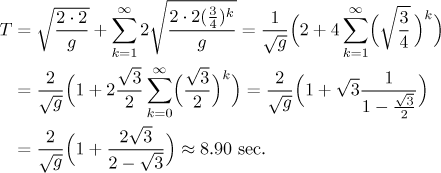
Problem: A certain rubber ball when dropped on a hard floor bounces back up to the 3/4 of the height from which it was dropped. We decide to ignore effects of elasticity and small-scale phenomena. Find the distance that the ball travels if it is dropped from the height of 2 meters.

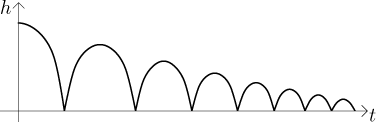
Solution: The ball starts bouncing and bounces and bounces and bounces, the height of the bounce is getting smaller and smaller. Our assumption means that even when the jumps are very tiny, the mechanism stays the same, and so the ball actually bounces infinitely many times.

Thus to find the total distance of travel we have to sum up a series. To see which one we will have a closer look at the heights that the ball reaches in its jumps. Obviously we use the fact that each jump has 3/4 of the height of the previous one.

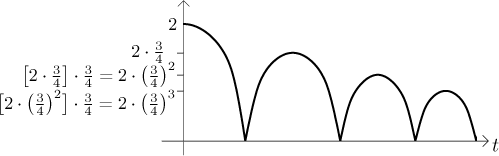
Thus we see that the first leg is a bit special (it is only one way), but then we add two times terms that obviously form a geometric series.

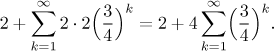
Since the base q = 3/4 satisfies |q| < 1, this series converges and we have

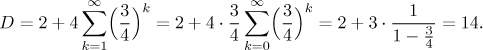
We ignored some fairly substantial influences. A "real" ball has some elasticity and gets deformed at the moment of bounce. When the bounces are really small, they do not even lift the ball off the floor, they just stretch it a bit up, then it gets squeezed a bit and the resistance to this is so strong that the ball shortly stops. However, this happens only if the jumps are very tiny and that did not contribute very much to the total displacement calculated above. Thus the error is small and the figure 14 meters is a rather good approximation.

Bonus: We return back to the idea of the ball making infinitely many jumps. How long does it take? First, we will find how long does it take for the ball to fall to the floor when dropped from the height h. We will ignore the effect of air resistance since for a bouncing ball it does not have a substantial influence. The starting velocity is zero (the ball is on the top of its jump), so we get

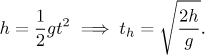
Next we claim that the time on the upward leg is the same as the time on the downward leg. Let's investigate one jump. The initial velocity (at the ground) v₀ decreases as the ball rises, eventually becoming zero on the top. If t₀ is the time it takes, we get the formula v₀ = g⋅t₀. Then the ball speeds up down and eventually reaches velocity v₁ at the moment of impact. Denoting by t₁ the time it takes we get the formula v₁ = g⋅t₁.

Now we look at this situation through the eyes of energy (and recall that we ignore loses like friction). The kinetic energy related to the velocity v₀ first entirely changes into potential energy (top of the jump) and then back to kinetic energy (we take the ground as the zero level for potential energy). From thsi it follows that v₀ = v₁, hence the formulas above yield t₀ = t₁.

We now know the times it takes to cover all the legs in the above picture, so we sum them up.

Back to Solved Problems - Summing up series