Convergence of sequences of functions: Methods survey

We are given a sequence of functions { f_k(x)} and we assume that the intersection of all their domains is not empty. Usually we ask about two things: What is the limit of this sequence and whether it converges uniformly at least somewhere.

Question 1: Investigate (pointwise) convergence of the given sequence of functions.
Solution: Consider a general x from the intersection of domains, take it as a fixed parameter and evaluate the limit of the sequence of real numbers { f_k(x)} for k going to infinity.
For some x this will diverge. For some x this limit converges, call the resulting number f (x). The set of all x for which this limit converges forms the region of convergence, on it we have the function f obtained as above and we say that the sequence { f_k} converges to f there.

Question 2: Investigate uniform convergence of the given sequence of functions.
Solution: First, find the limit f of { f_k} as above.
Next, guess a set M (a subset of the region of convergence) on which you suspect uniform convergence. Typically you start with the region of convergence, or the region of convergence without small neighborhoods of its endpoints.
For a fixed k, evaluate

M_k = sup{| f (x) − f_k(x)|,  x from M }.

If M_k→0 for k going to infinity, uniform convergence on M is proved.
If not, then most likely the set M is too ambitious. Try to guess a smaller set, analysis of the suprema above may help in identifying which parts of the original M caused troubles.

Example: Investigate convergence of the sequence

Solution: First we investigate convergence. We consider x to be a parameter and evaluate limit in k.

This limit existed for all values of x, so the region of convergence is the whole real line and the given sequence converges there to the function f (x) = x².

Is this convergence uniform? We look at the difference. For a fixed k one gets

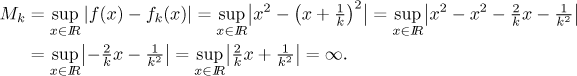
Since all suprema are infinity, there is no way they can go to zero and thus we do not have uniform convergence on the whole real line. Obviously the problem is that x is allowed to become arbitrarily large. Thus we guess that we have a better chance if we investigate uniform convergence on a closed interval M = [−a,a] for an arbitrary positive a. Now we get

When we send k to infinity, then M_k tends to zero, which proves that the given sequence { f_k(x)} converges to f (x) = x² uniformly on every interval of the form M = [−a,a] for positive a.
In fact, a similar argument shows a somewhat more general and simpler to state fact that the convergence is uniform on every bounded subset of real numbers.

For other examples see Solved Problems - Series of functions.

Convergence of series of functions
Back to Methods Survey - Series of functions